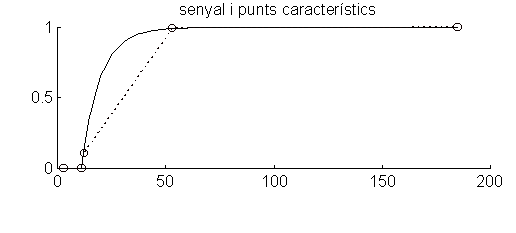
Fig. 1 Respuesta de un sistema de primer orden i su representación.
En esta sección, con el objetivo de mostrar la utilidad de la representación cualitativa, se analizan diversas señales simuladas. En estos ejemplos puede verse como las características de cada señal quedan bien reflejadas en su representación. Se ha obtenido la representación de la respuesta a un escalón de sistemas lineales de diversos ordenes, estables i inestables. También se han representado las señales correspondientes a un sistema no lineal en diferentes situaciones. En todos los casos la representación es válida para describir adecuadamente el comportamiento de las señales.
Los ejemplos presentados permiten llegar a la conclusión que se pueden hacer los mismos comentarios de cada caso observando las señales o a partir de sus representaciones. Esto indica que las representaciones son válidas para describir adecuadamente las señales, con la ventaja que pueden ser fácilmente utilizadas por herramientas de Detección o Diagnóstico como Sistemas Expertos o Clasificadores.
Los ejemplos con señales que proceden de sistemas lineales, con un abanico suficientemente amplio de situaciones, permite ver como se pueden representar adecuadamente dinámicas muy diferentes, incluyendo discontinuidades i estados estacionarios. En los ejemplos con señales procedentes de un sistema no lineal se puede ver como se representan los cambios en la dinámica del sistema; este hecho es importante si se tiene en cuenta que uno de los objetivos de la representación es facilitar la Detección.
Análisis de respuestas de sistemas lineales a un escalón
En estos primeros ejemplos se han estudiado representaciones de la respuesta a un escalón de sistemas lineales de primer orden, de segundo orden, de orden superior, estables e inestables, con oscilaciones i sin ellas, y de tipo 1. Puede decirse que este conjunto de señales representados incluye todas las dinámicas de los señales que provienen de sistemas lineales. Los resultados muestran como los diferentes comportamientos de los señales queden bien representados. Cabe remarcar que el objetivo de estos ejemplos es mostrar como se representan las diversas dinámicas de las señales y no intentar identificar los sistemas de los cuales provienen.

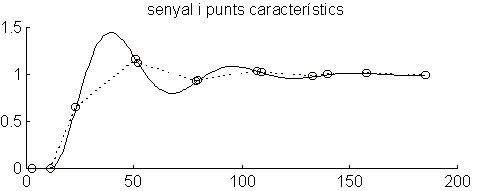
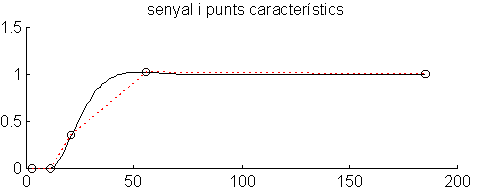
Fig. 2 Respuestas de sistemas de segundo orden y sus representaciones
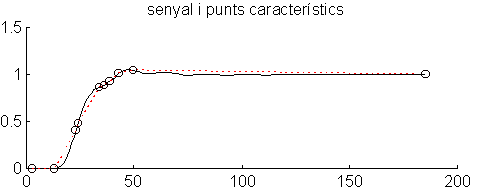
Fig. 3 Respuesta de un sistema de orden 4 i su representación.
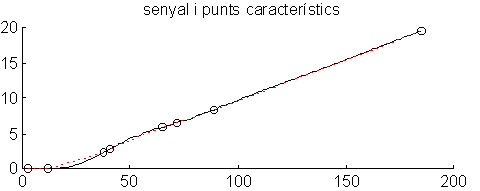
Fig. 4 Respuesta de un sistema de tipo 1 y su representación.
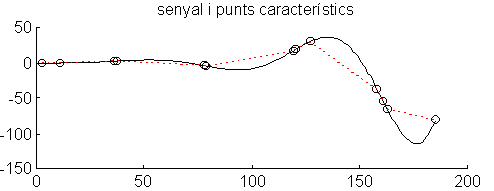
Con el objetivo de probar la utilidad de la representación en episodios también en sistemas no lineales, se propone estudiar un modelo simplificado conocido como de depredador-presa en el cual los resultados son señales periódicas. En sistemas no lineales las mismas variaciones no siempre producen los mismos efectos, la evolución del sistema depende de las condiciones iniciales i de los momentos en los que se producen los cambios.
El modelo conocido como depredador-presa es un modelo muy sencillo de interacción entre dos poblaciones que podemos suponer de peces: los buenos para el consumo o presas (N1(t)), i los que no lo son o depredadores (N2(t))
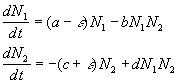
donde a, b, c i d son constantes positivas i e es una constante positiva que representa la intensidad de la pesca suponiendo que es la misma para todos los tipos de peces. Este modelo da como resultado funciones periódicas para N1 i N2, demostrándose que el valor medio de las variables en un período es, si los coeficientes son positivos:
Esto explica que la pesca sea beneficiosa para la población de presas i perjudicial para la población de depredadores siempre que la pesca sea moderada (e < a). En caso contrario (e>=a), la población de presas (N1) decrece hasta desaparecer i, en consecuencia, también desaparece la población de depredadores (N2). Por otra parte, en este modelo las condiciones iniciales determinan la futura evolución del sistema; la influencia de la pesca, por tanto, varia en función del instante en el que se introduce, ya que representa un cambio de modelo, i la evolución futura depende de las condiciones iniciales para el nuevo modelo.El interés de este modelo, que también ha sido estudiado en [Ayrolles, 1996], como ejemplo se fundamenta en que:
Para obtener los resultados a partir del modelo, este se puede simular utilizando SIMULINK. Los valores de los parámetros utilizados seguramente no se asemejen a los de un sistema real, pero este no es el objetivo de el estudio. El objetivo final es ver como el parámetro e influye en la dinámica del sistema a partir del estudio de las representaciones de los resultados de la simulación.es no lineal. los resultados son normalmente señales periódicas. el inicio de la pesca supone un cambio en la dinámica del sistema. Este cambio representa, en muchas ocasiones, discontinuidades en las señales. el periodo i los valores medios de las señales dependen de la intensidad de pesca e. los resultados pueden dejar de ser señales periódicas a partir de ciertos valores de la intensidad de pesca e.

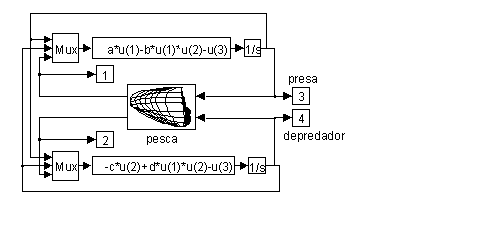
Los valores de los parámetros del modelo utilizados en las simulaciones son:
en las unidades correspondientes. En este caso se ha escogido como a unidad de tiempo el día.Se propone estudiar el sistema en las siguientes situaciones:
Modelo sin pesca con diversas condiciones iniciales. En este caso puede verse que con condiciones iniciales cercanas a los valores medios las oscilaciones son muy débiles, mientras que para condiciones iniciales alejadas de los valores medios las oscilaciones tienden a crecer en amplitud, aunque no cambie el periodo.
En total se proponen 14 casos. En la Taula -1 se pot veure la numeración
donada a cada uno con las condiciones iniciales i las características
de la pesca en cada uno de ellos. En todos los casos puede simularse un
periodo de 10 años con un tiempo de muestreo de una semana.
| CASO |
|
|
|
|
|
1
|
|
|
|
|
|
2
|
|
|
|
|
|
3
|
|
|
|
|
|
4
|
|
|
|
|
|
5
|
|
|
|
|
|
6
|
|
|
|
|
|
7
|
|
|
|
|
|
8
|
|
|
|
|
|
9
|
|
|
|
|
|
10
|
|
|
|
|
|
11
|
|
|
|
|
|
12
|
|
|
|
|
|
15
|
|
|
|
|
|
14
|
|
|
|
|
Taula -1 Casos a estudiar.
Los intervalos característicos (Fig. 7) para la representación son los mismos para las dos señales y se han escogido de forma experimental a partir de la observación de la primera y segunda derivadas de las señales.
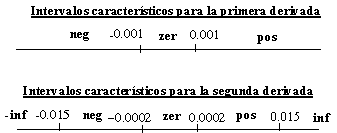
Fig. 7 Intervalos característicos para las dos señales.
En las Fig. 8 i Fig. 9 puede verse detalladamente la obtención de la representación para una de las señales en uno de los casos estudiados (caso 4).
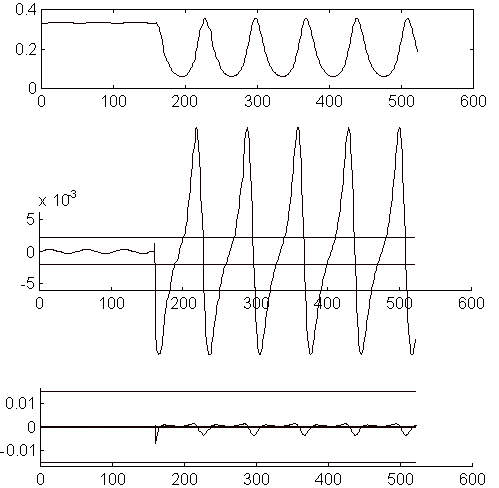
Fig. 8 Evolución de la población de depredadores, primera
derivada,
segunda derivada i límites para N1(0)=1, N2(0)=0.33 i e=0.005
a partir de t=1000.
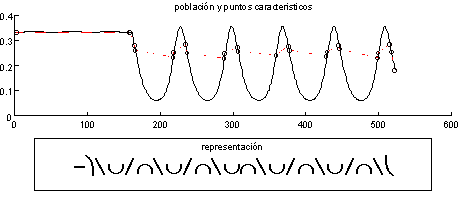
Fig. 9 Punts característics i representación per al señal de la Fig. 8.