6.7 Una representación basada en el formalismo
general
En esta sección se describirá una representación de
las señales basada en episodios que tiene en cuenta algunos aspectos
que no han estado considerados en otras representaciones descritas anteriormente.
Esta representación describe la dinámica de las señales
entrando, en est sentido, en la misma familia que las otras. Los rasgos
distintivos de esta representación, detallados a lo largo de esta
sección se pueden resumir en:
-
Utilización de una sola función característica. Esto
simplifica la obtención de la representación i al mismo tiempo
simplifica el resultado final facilitando su interpretación i utilización.
Estas ventajas dependen, obviamente, a una elección adecuada de
esta función característica. De nada sirve obtener una representación
con pocos episodios si estos no son suficientemente significativos.
-
Representación explícita de los periodos de estabilidad.
Los periodos en los que un señal permanece estable en un determinado
valor o con pequeñas variaciones a su alrededor son, en procesos
controlados, los más largos i/o frecuentes. Por lo tanto, es importante
que en la representación de las señales estos periodos queden
reflejados en forma de episodios.
-
Representación explícita de las discontinuidades. Al igual
que los periodos de estabilidad, las discontinuidades en la señal
también pueden expresar muchas cosas acerca de el funcionamiento
de los procesos. Por esto es conveniente que en la representación
de las señales las discontinuidades aparezcan explícitamente,
en forma de episodios.. En señales muestreados las discontinuidades
aparecen en forma de 'cambios más grandes de lo normal' i usualmente
en un único instante de tiempo; en señales filtrados o que
han sufrido algún tratamiento previo, pero, pueden quedar repartidas
a lo largo de un intervalo de tiempo.
-
Obtención de datos numéricos. Los episodios ofrecen una representación
simplificada de las señales. Por lo tanto, los datos numéricos
obtenidos a partir de los episodios pueden aportar información útil
que complemente la información cualitativa con un nivel de abstracción
suficiente. El nivel de abstracción de estos datos cuantitativos
será, pues, igual al de los propios episodios.
Función característica
La función característica escogida en esta representación
es la segunda derivada de la señal, ya que, como se verá,
es suficiente para representar la dinámica de las señal de
forma simple i al mismo tiempo completa. Puede decirse que los cambios
importantes en la dinámica de una señal se producen en los
extremos, en los puntos de inflexión i en las discontinuidades.
Pero los extremos, aunque queden determinados por la primera derivada,
son provocados por la segunda derivada, i podemos saber de su existencia
(aunque aproximada) conociendo la derivada en los puntos de inflexión.
Observando la segunda derivada se pueden conocer también las discontinuidades
en la señal i en la primera derivada. Por lo tanto, es razonable
tomar como función característica la segunda derivada.
En la señal de la Fig. 1 puede verse una señal de prueba
que incluye las respuestas a un escalón de un sistema de segundo
orden y uno de primer orden separados por una discontinuidad. La dinámica
de la señal queda bien representada en su segunda derivada. Las
discontinuidades en la señal i en su primera derivada provocan picos
y valores anormales en la segunda derivada.
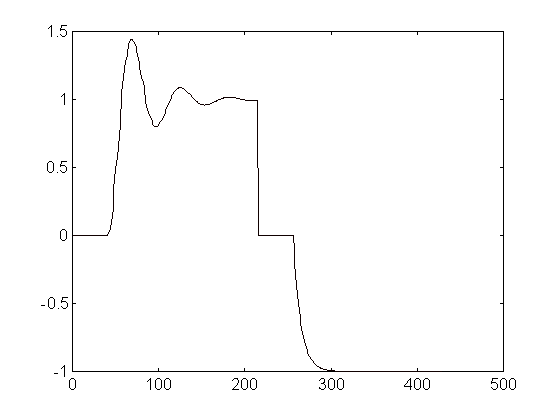
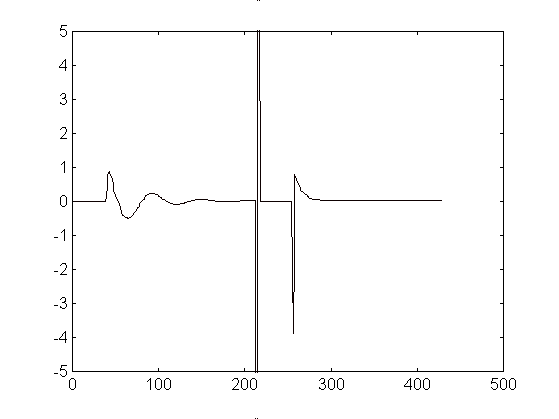
Fig. 1: Señal con discontinuidades i su segunda derivada.
Notación: ddx representa la segunda derivada de la señal
i [ddx] su valor cualitativo.
Intervalos característicos
Los intervalos característicos deben permitir cualificar, a partir
de la función característica, las diversas situaciones en
las que puede encontrarse la señal i que deben aparecer en su representación.

Fig. 2 Intervales característics.
En esta representación se escogen 5 intervalos característicos
(Fig. 2), de forma que sirvan para describir correctamente los cambios
de dinámica de la señal. El intervalo central, centrado en
cero, representa una zona de inflexión o de estabilidad, que sea
suficientemente ampliopara que los episodios con segunda derivada nula
(de estabilidad o de inflexión) aparezcan significativamente en
la representación de la señal. Los intervalos -inf i inf
sirven para describir discontinuidades, las cuales provocan valores extremos
en la segunda derivada.
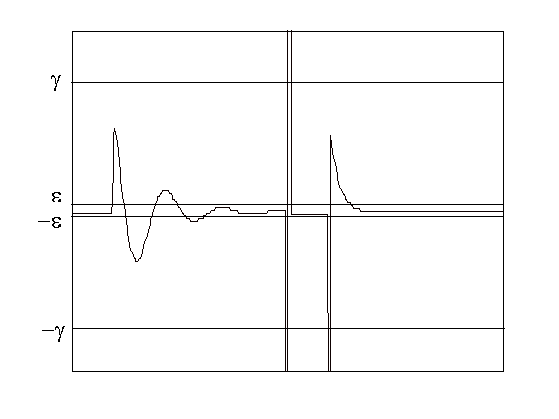
Fig. 3 Límites de los intervalos característicos.
Instantes característicos
Aunque la función característica es la segunda derivada,
los instantes característicos no son propiamente los puntos de inflexión.
Pueden representar diversos cambios:
-
Inicio de un episodio de inflexión.
-
Fin de un episodio de inflexión.
-
Inicio de un episodio de discontinuidad.
-
Fin de un episodio de discontinuidad.
-
Punto de inflexión, sólo cuando el valor cualitativo de la
función característica pasa directamente de pos a neg o a
la inversa.
Estos cambios dependen del cambio de intervalo característico
que se produce en la segunda derivada. Los instantes característicos
sólo aportan información sobre el instante de tiempo en el
que se produce algún cambio Esta información, pero, puede
ser aprovechada para obtener otros datos, numéricos o cualitativos,
de la señal en estos instantes de tiempo.
Clasificación fundamental
La representación se basa en una sola función característica
con cinco intervalos característicos, la clasificación fundamental,
por lo tanto, consta de cinco tipos básicos de episodios que poden
ser representados de la siguiente forma:
Ç : [ddx] = neg
È : [ddx] = pos
- : [ddx] = zer
û : [ddx] = inf
é : [ddx] = -inf
Fig. 4 Tipos básicos en la clasificación fundamental.
Pero es evidente que estos cinco tipos no sirven para describir cualquier
dinàmica de forma suficientemente específica. Pueden encontrarse
señales con comportamientos muy diferentes que den lugar a la misma
representación (Fig. 5).
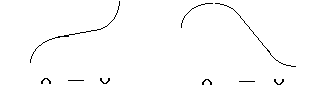
Fig. 5 Señales diferentes con la misma representación.
Per obtener una mejor representación se añaden características
auxiliares cualitativas que permiten enriquecer la clasificación
fundamental para obtener la clasificación útil.
Características auxiliares cualitativas
Como características auxiliares cualitativas se escogen los dos
valores cualitativos de la derivada en los dos extremos del episodio ([dxl]
i [dxr]), obtenidos mediante una cualificación en tres valores de
la derivada en los instantes característicos que delimitan el episodio
:

Fig. 6 Valores cualitativos de la derivada.
Esta cualificación debe hacerse de forma que el intervalo zer
sea significativo i esté en concordancia con el intervalo zer escogido
para la segunda derivada. Las características auxiliares no influyen
en la detección de los instantes característicos ni en la
duración temporal de los episodios, pero permiten establecer una
clasificación (la clasificación útil) más expresiva.
La utilización de la derivada en los instantes característicos
permite representar mejor la dinámica de la señal i tener
una idea de como la segunda derivada provoca variaciones significativas
en la pendiente de la señal a lo largo de un episodio .
Clasificación útil
La clasificación útil correspondiente a tener en cuenta
la clasificación fundamental i las características auxiliares
da como resultado trece tipos diferentes de episodios, representados por
los símbolos que pueden verse en la Fig. -7.
ù é æ Ç ö \ - / è È
ø û ë
Fig. -7 Símbolos que representan los 13 tipos de episodios.
Estos trece tipos están determinados por los valores cualitativos
de la segunda derivada ([ddx]) i de la primera derivada en los instantes
característicos que limitan el episodio por la derecha ([dxr]) i
por la izquierda ([dxl]). La clasificación no tiene en cuenta todas
las posibles combinaciones de estos tres valores. Unicamente se distinguen
aquellos casos que son posibles. En las tablas Tabla 1 a Tabla 5 pueden
verse todas las combinaciones i, en su caso, el tipo de episodio asociado
a cada uno.
|
ddx = -inf
|
|
[dxr]
[dxl]
|
neg
|
zer
|
pos
|
|
Neg
|
ù
|
**
|
**
|
|
Zer
|
ù
|
**
|
**
|
|
Pos
|
é
|
é
|
**
|
Tabla 1
|
ddx = neg
|
|
[dxr]
[dxl]
|
neg
|
zer
|
pos
|
|
neg
|
ö
|
**
|
**
|
|
zer
|
ö
|
æ *
|
**
|
|
pos
|
Ç
|
æ
|
æ
|
Tabla 2
|
ddx = zer
|
|
[dxr]
[dxl]
|
neg
|
zer
|
pos
|
|
neg
|
\
|
- *
|
/ *
|
|
zer
|
\ *
|
-
|
/ *
|
|
pos
|
\ *
|
- *
|
/
|
Tabla 3
|
ddx = pos
|
|
[dxr]
[dxl]
|
neg
|
Zer
|
pos
|
|
neg
|
è
|
è
|
È
|
|
zer
|
**
|
è *
|
ø
|
|
pos
|
**
|
**
|
ø
|
Tabla 4
|
ddx = +inf
|
|
[dxr]
[dxl]
|
neg
|
Zer
|
pos
|
|
neg
|
**
|
ë
|
ë
|
|
zer
|
**
|
**
|
û
|
|
pos
|
**
|
**
|
û
|
Tabla 5
Los tipos representados con un asterisco (*) representan combinaciones
que, en principio, no deben aparecer nunca, pero que pueden aparecer si
no se cualifica bien la primera derivada, en señales mal filtrados,
o si existe algún retardo entre la primera i la segunda derivada.
Los tipos representados con dos asteriscos (**) son los considerados imposibles.
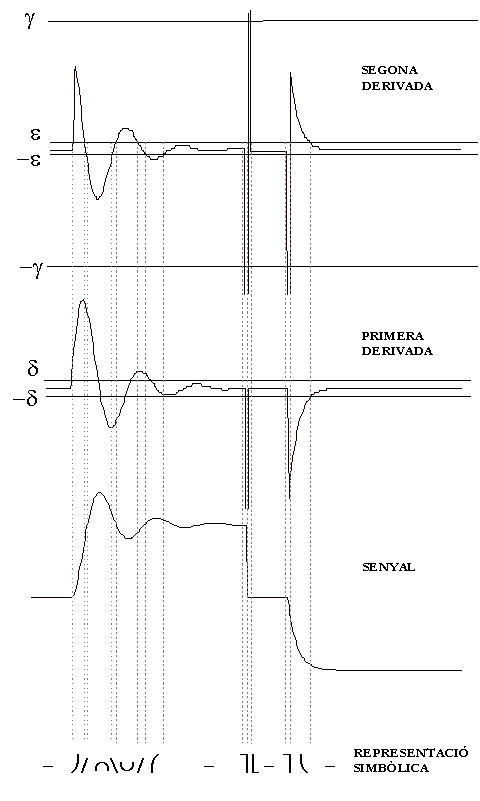
Fig. 8 Representación de la señal de la Fig. 1.
En la Fig. 8 puede verse detalladamente la representación resultante
de la señal de la Fig. 1. Las discontinuidades en la señal
i en la primera derivada quedan representadas explícitamente, hecho
que también sucede con los periodos de estabilidad. Así mismo,
pueden verse los episodios de inflexión que aparecen en los cambios
de signo de la segunda derivada.
Características auxiliares cuantitativas
Las características auxiliares cuantitativas deben utilizarse
para complementar la representación cualitativa. El hecho de calcular
estas datos numéricos a partir de los episodios y los instantes
característicos de la representación implica una simplificación
i, por lo tanto, un mayor grado de abstracción en la información
numérica obtenida. A continuación se proponen algunas de
estas características auxiliares que pueden ser útiles en
algunos casos.
-
Valor de la señal en los instantes característicos: Si los
instantes característicos que limitan un episodio son tl
i tr, el valor de la señal x(t) en estos instantes será
x(tl) i x(tr), respectivamente. El par de puntos
(tl,x(tl)) i (tr,x(tr)) pueden
definirse como puntos característicos del episodio .
-
Aproximación per una función cúbica: A partir de los
puntos característicos i del valor de la derivada en estos puntos
puede encontrarse una función cúbica que represente una aproximación
de la señal en el episodio :
a(t)=a3·t3+a2·t2+a1·t+a0
x(tl)= a3·tl3+a2·tl2+a1·tl+a0
x(tr)= a3·tr3+a2·tr2+a1·tr+a0
dx(tl)= 3a3·t2+2a2·t+a1
dx(tr)= 3a3·tr2+2a2·tr+a1
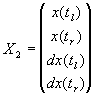 ;
; 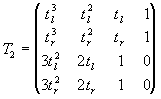 ;
; 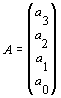 ;
;
A=T2-1X2
Esta aproximación no aporta directamente mucha información
significativa, pero representa una simplificación de la información
numérica a partir de la cual pueden encontrarse otros datos.
-
Otros datos que pueden ser útiles son los valores máximo
i mínimo en los episodios de tipo Ç o È , la distancia
entre el máximo o mínimo i la recta de soporte o el área
entre la señal i la recta de soporte.
Ejemplo comparativo
Para ilustrar las diferencias existentes se han obtenido las diferentes
representaciones de una señal, dando como resultado las figuras
Fig. 10 a Fig. 13.
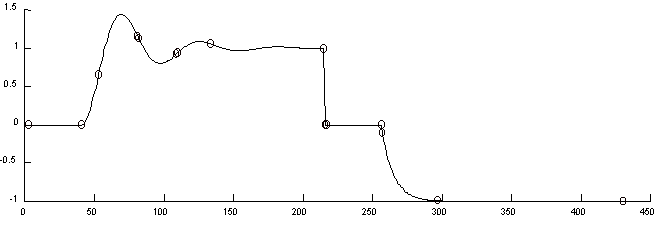
Fig. 10 Señal, instantes característicos i representación.
Obtenidos utilizando la nueva representación.
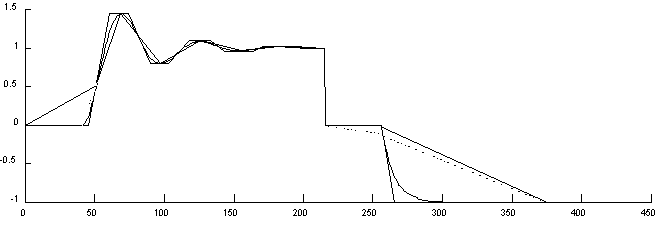
DABCDABCDABCGC según [Cheung and Stephanopoulos, 1990]
A*B*D*C*A*B*D*C*A*B*D*CD*C* según Ayrolles, 1996]
Fig. 11 Señal y representación triangular.
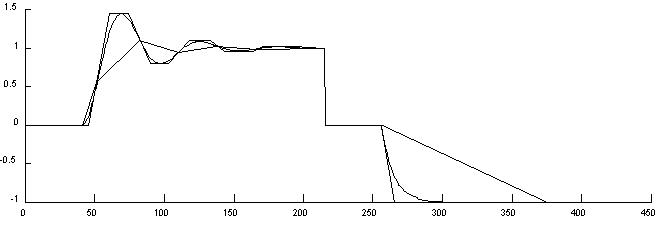
Fig. 12 Señal y representación trapezoidal.
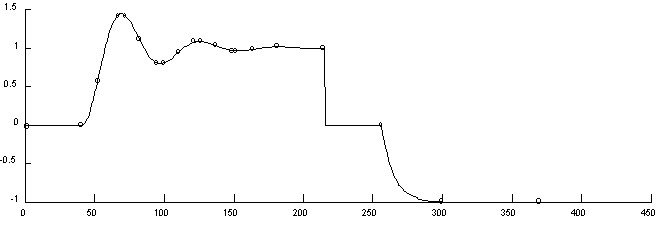
ABDAGEABDAGEABDAAEA
Fig. 13 Señal, instantes de separación de los episodios
i representación. Obtenidos utilizando TDL







![]() ;
; ![]() ;
; ![]() ;
;
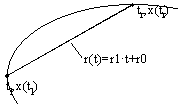
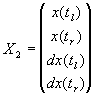 ;
; 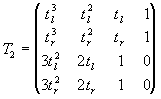 ;
; 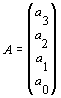 ;
;



