1

7.11 Grafos lógicos causales para el razonamiento diagnóstico En esta sección se presenta un modelo general para la inferencia causal abductiva. Este modelo se en codificar dependencias causales entre síntomas mediante grafos causales lógicos, llamados grafos AND/OR/NOT. Se presenta una representación uniforme simple para grafos causales con lógica binaria. Los nodos de los grafos representan síntomas, formalmente equivalentes a formulas proposicionales, y las uniones representan relaciones causales. Básicamente, la relación causal permitida puede reflejar las operaciones lógicas básicas, conjunción (AND), disyunción (OR) y negación (NO). La estructura del grafo representa las dependencias causales entre los eventos. Pueden usarse tanto para modelado del comportamiento de sistemas como en inferencia diagnóstica.

Una vez construido el modelo de dependencias causales y echa la asignación inicial de manifestaciones observadas a los nodos del grafo, puede empezarse el procedimiento diagnóstico. La inferencia diagnóstica se basa en inferencia abductiva que toma la forma de procedimiento de búsqueda aplicado al grafo. Este enfoque es más general y potente que los presentados y puede considerarse como una extensión de la aplicación de árboles de fallos al razonamiento de diagnóstico.

Síntomas, conexiones lógicas causales y estructura del grafo

En los términos técnicos, un síntoma denota normalmente una característica de un sistema que ocurren en un tiempo. El problema importante para explicar comportamientos defectuosos en sistemas técnicos es el conocimiento de la relación causal entre los síntomas que ocurren en el sistema.

Los estados de un síntoma pueden ser tres, verdadero (si se sabe que ocurre), falso (si se sabe que no ocurre), o desconocido. En este trabajo los síntomas son considerados más bien como una categoría lingüística útil mas que como un término lógico precisamente definido; sin embargo, desde el punto de vista lógico pueden considerarse a menudo como descritos mediante formulas lógicas. Para la representación mediante un conjunto extendido de valores, los síntomas pueden ser considerados como variables que toman valores de un conjunto especificado previamente; en nuestro caso el conjunto es precisamente , pero si es necesario, puede extenderse arbitrariamente a varios elementos.

Pueden considerarse diversas categorías de síntomas. En primer lugar, hay manifestaciones externas, que normalmente denotan síntomas de fallo y comportamientos anormales o defectuosos del sistema considerado. Estos constituyen la principal salida observable del sistema bajo el diagnóstico. El conjunto de manifestaciones se denotará como .

En segundo lugar se distingue un conjunto de síntomas de causa inicial. Una causa inicial es un síntoma sin ninguna razón visible o para el cuál no se busca ninguna causa extensa o explicación. Las causas iniciales pueden dividirse en varias subcategorías, por ejemplo fallos de componentes, acciones de control, condiciones externas, etc., Todas ellas son consideradas como diagnósticos elementales. El conjunto de diagnósticos elementales se denota como .

La tercera categoría de síntomas son los (otros) síntomas intermedios; éstos son simplemente los, directamente observables o no, que no son manifestaciones (M) ni diagnósticos elementales (D). El conjunto de tales síntomas se denotará por .

El conjunto de todos los síntomas será denotado por N, donde . Finalmente, para clarificar, se supone que los tres conjuntos que componen N son disjuntos dos a dos.

Teniendo en cuenta problemas prácticos de diagnóstico, cualquier elemento de N puede considerarse como síntoma, evento, variable binaria, hecho o fórmula proposicional. De este modo, son posibles varias formas de notación; un síntoma observado puede denotarse como n=verdad, n=1 o simplemente n, mientras, su ausencia puede denotarse como n =falso, n=0 o .

Por el bien de la representación gráfica se supone que las relaciones causales entre los síntomas se especifican mediante la representación del grafo. Cada nodo del grafo representa un síntoma específico . Siempre que existe una relación causal entre dos nodos, n y n´, existe un arco dirigido que apunta de n al n´. El significado del arco es que n causa n´. Utilizando notación lógica, la semántica de una conexión entre dos nodos se define n Æ n´, es decir, si n se vuelve verdadero entonces también n´ se vuelve necesariamente verdadero. En \cite{Ligeza:96}, \cite{Fuster:96} pueden encontrarse una definición más detallada y algunas extensiones.

Los nodos del grafo se conectan mediante los llamados componentes funcionales. Un componente funcional conecta uno o varios nodos de entrada con exactamente un nodo de salida. Un componente funcional f se representa como un triplete , donde n es el nodo de salida, fun es la función realizada y son los nodos de entrada. Básicamente se supone que hay tres tipos de componentes funcionales que corresponden a las funciones lógicas conjunción (AND), disyunción (OR) y negación (NO). Por consiguiente, existen tres tipos de componentes funcionales, conjunción lógica de k entradas , disyunción lógica de k entradas , y negación lógica de exactamente un nodo de entrada . Para simplificar, los nodos de salida correspondientes a componentes funcionales se nombran después de los componentes respectivos, es decir, nodos AND, OR y NO , respectivamente.

Un grafo lógico causal AND/OR/NOT es una estructura , donde N es el conjunto de nodos del grafo, , y F es un conjunto de componentes funcionales que definen las conexiones entre los nodos. Además, se supone que no hay ningún arco que apunta desde los nodos especificados en M (sólo son nodos de salida, las manifestaciones son nodos finales), no hay ningún arco que apunta a los nodos de D (los diagnósticos elementales son iniciales o sólo nodos de entrada), y no existe en el grafo ningún lazo cerrado. Además, puede considerarse que cada nodo tiene por lo menos un arco de entrada o salida. En [Ligeza, 1996c], [Fuster, 1996] pueden encontrarse otras consideraciones y algunas extensiones.

La interpretación de la definición anterior es directa. Hay un arco dirigido del nodo n al nodo n´ siempre que n cause n´. También es posible que existan varios arcos que apuntan de varios nodos a n; en este caso los arcos denotan un elemento funcional. En este caso, si la ocurrencia de cualquiera de los síntomas representado por estos nodos es suficiente para que n se vuelva verdadero, n es un nodo OR y los arcos (no marcados de ninguna manera específica) forman el componente funcional de tipo OR. Si los síntomas sólo causan n al ocurrir juntos, entonces todos los arcos de a n se une por un arco "horizontal" especial y forman un componente funcional de tipo AND; el nodo n será entonces un nodo AND. Por último, habrá un arco llamado NOT desde hasta n siempre que la ausencia del síntoma definido en (su negación) cause n.En la siguiente figura se presenta un ejemplo de grafo causal AND/OR/NOT.

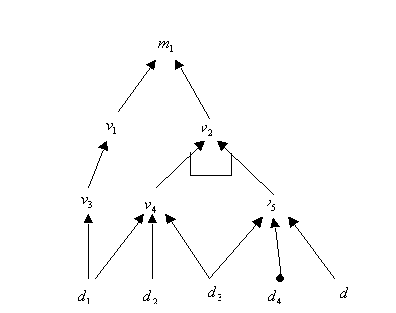
El único nodo AND es , la conexión entre y es de tipo NO. El grafo causal AND/OR/NOT anterior es similar en estructura a los clásicos grafos Y/O usados en solución de problemas [Nilsson, 1980]. Las diferencias principales consisten en la dirección e interpretación de los arcos (aquí son posibles diversas extensiones diferentes de la interpretación causal básica; ver por ejemplo las conexiones MAY en [Console et al, 1989], [Console and Torasso, 1992]; ver también [Fuster, 1996]) y los nodos (aquí un nodo inicial significa sólo una posibilidad de solución). La aplicación del grafo también es diferente. Una extensión visible la constituye la admisión de conexiones NO. Además, un "grafo solución" ,en solución de problemas clásica, constituye sólo una "posible justificación" (para ser validada posteriormente) para el fallo observado. Los grafos causales AND/OR/NOT también constituyen un refinamiento de los árboles de fallos [Barlow and Lambert, 1975] y los grafos causales usados en diagnóstico basado en modelo- orientado hacia la búsqueda directa de diagnósticos.

Los grafos causales AND/OR/NOT parecen constituir un formalismo uniforme, intuitivo y potente. De hecho pueden englobar la mayoría de los formalismos presentados hasta ahora. Como veremos, el procedimiento de inferencia también es uniforme y relativamente simple.

Una declaración del problema diagnóstico y su solución

Un problema diagnóstico existe si por lo menos se observa un fallo. Se supone que los fallos a ser diagnosticados se especifican mediante algunas manifestaciones (positivas o negativas). Consideremos un grafo causal AND/OR/NOT G. La formulación del problema diagnóstico también tiene en cuenta algunas posibles observaciones que proporcionan mas información al sistema diagnóstico.

Un problema diagnóstico es un 5-tuple donde y son las manifestaciones de fallo a ser diagnosticadas, verdaderas y falsas respectivamente, y donde y son las observaciones auxiliares que especifican qué síntomas son verdaderos y falsos; , , y . Los conjuntos de manifestaciones verdaderas y falsas proporcionan la definición del fallo y debe ser explicadas por todos los diagnósticos encontrados, mientras que las observaciones auxiliares proporcionan información que puede usarse para guiar, pedir y refinar la búsqueda. Cualquier diagnóstico debe ser consistente con las observaciones.

Para resolver problema diagnóstico debe buscarse un conjunto de posibles síntomas de causas iniciales que expliquen (justifiquen) los fallos especificados mediante los valores de las manifestaciones en curso. Básicamente, la búsqueda para los posibles diagnósticos (no necesariamente los mínimos) puede ser cualquier procedimiento sistemático de búsqueda en grafos [Nilsson, 1980] teniendo en cuenta el carácter específico del grafo definido (la interpretación de nodos como síntomas; algunos de ellos pueden conocerse como verdadero/falso a priori) y sus elementos (las conexiones AND, OR y NO). Así, informalmente hablando, el problema de encontrar posibles (potencial) diagnósticos es equivalente a encontrar un conjunto (conjunto mínimo) de síntomas iniciales que definan componentes defectuosos, acciones de control y signos externos, tales que la combinación de causas iniciales implique la anormalidad observada. De hecho, un diagnóstico puede ser cualquier combinación consistente de valores de síntomas de D, justificando el comportamiento anormal observado con respecto a la estructura del grafo y consistente con las observaciones.

La búsqueda de diagnósticos potenciales se realiza hacia atrás. Para un conjunto dado de manifestaciones se tiene que suponer y explorar el posible estado de los nodos anteriores que implican el estado observado de las manifestaciones. Destaquemos que cualquier nodo puede tomar uno de los siguientes estados: conocido (o supuesto) como verdadero, conocido (o supuesto) como falso o desconocido. La asignación en curso de valores de verdad a los síntomas del grafo (posiblemente no a todos ellos) determina el estado actual de la búsqueda.

Formalmente, para definir el estado de la búsqueda, se introduce una cartografía de la forma: asignando a cualquier síntoma su estado actual. En la práctica, el estado inicial de búsqueda esta definido por la especificación de las manifestaciones verdaderas y falsas ( y ) y las observaciones de síntomas verdaderos y falsos ( y ). Durante la búsqueda se supone que algunos nuevos nodos se vuelven verdaderos o falsos; así, en cualquier fase de la búsqueda el conjunto de nodos verdaderos es de la forma (donde ) y el conjunto de nodos falsos es (donde ).

Los síntomas de valor desconocido no se representan explícitamente en conjunto. Se supone que cualquier estado definido por y es consistente, es decir , la intersección de síntomas verdaderos y falsos está vacía. Aún más, también se supone que cualquier conjunto de estado es máximo con respecto a la posibilidad de propagación de información. Siempre que se evalúe algún nuevo nodo o se suponga que es verdadero/falso, esta información influye en el estado de la búsqueda. Las reglas de propagación se definen a continuación:

Propagación hacia delante: (causalidad, interpretación lógica simple)

Nodo OR verdadero: si por lo menos uno de los predecesores de un nodo OR es verdad, entonces el valor del nodo OR se vuelve verdadero,

Nodo AND falso: si por lo menos uno de los predecesores de un nodo AND es falso, entonces el valor del nodo AND se vuelve falso.

nodo NO verdadero: si un predecesor de un nodo NO es falso, entonces el valor del nodo NO se vuelve verdadero,

nodo NO falso: si un predecesor de un nodo NO es verdad, entonces el valor del nodo NO se vuelve falso.

Propagación hacia delante: (causalidad, interpretación lógica simple; se suponen los predecesores de un nodo para ser todas las causas directas para él)

Nodo OR falso: si todos los predecesores de un nodo OR son falsos, entonces el valor de este nodo OR se vuelve falso,

Nodo AND verdadero: si todos los predecesores de un nodo AND son verdad, entonces el valor de este nodo AND se vuelve verdadero.

Propagación hacia atrás: (causalidad, interpretación lógica simple)

Nodo OR falso: si un nodo OR es falso, entonces el valor de todos sus predecesores se vuelve falso,

Nodo AND verdadero: si un nodo AND es verdad, entonces el valor de todos sus predecesores se vuelve verdadero,

Nodo NO verdadero: si un nodo NO es verdad, entonces el valor de su predecesor se vuelve falso,

Nodo NO falso: si un nodo NO es falso, entonces el valor de su predecesor se vuelve verdadero.

Propagación hacia atrás: (causalidad, interpretación lógica simple; se suponen los predecesores de un nodo para ser todas las causas directas para él)

Nodo OR falso: si un nodo OR es falso, entonces el valor de todos sus predecesores se vuelve falso,

Nodo AND verdadero: si un nodo AND es verdad, entonces el valor de todos sus predecesores se vuelve verdadero.

Las reglas anteriores definen los principios de propagación de estado. Siempre que una regla sea aplicable, se genera un nuevo valor de síntoma; que pasa al nuevo conjunto de representación de estado en curso. En el caso que algún síntoma tome dos valores incoherentes, el estado inicial se considera incoherente para la propagación y no se tiene más en cuenta. En la práctica, esto tiene el efecto de failure y backtracking en Prolog.

Sea un conjunto cualquiera de síntomas de entrada junto con sus valores, donde especifica qué síntomas son verdad, y proporciona los síntomas falsos. Sea un estado del grafo que proporciona el conjunto de síntomas verdaderos y falsos, respectivamente. Se dice que el estado especificado por proviene de (o esta implicado por) si puede generarse de con respecto a las reglas de propagación anteriores; esto se denota como Ã.

Un cambio inicial del estado de un nodo es el resultado de la detección de un fallo; los nodos correspondientes de M cambian su estado de desconocido a verdadero o falso. Pueden realizarse mas cambios del estado actual del grafo como resultado de las siguientes operaciones:

suposición, formación de hipótesis que involucran a cierto nodo, realizada por un procedimiento de búsqueda de grafo; este cambio siempre es de desconocido a verdadero/falso,

realizando una prueba, sondeando (o sólo observando); una prueba asigna el valor verdadero/falso a uno o más nodos,

finalmente, después de cualquiera de estos cambios se aplican las reglas de la propagación para que se realicen todos los posibles cambios,

por último, pero no menos importante, si el nuevo estado es incoherente, alguna asunción sobre estado del síntoma debe retirarse (deshacerse) para recuperar la consistencia.

Con respecto a la definición de un grafo causal AND/OR/NOT y el problema diagnóstico, una solución al problema es cualquier combinación consistente de los valores de causas iniciales, tal que implique los funcionamientos defectuosos observados. El estado máximo implicado por un diagnóstico debe ser internamente consistente, y debe ser consistente con observaciones.

Sea un problema diagnóstico. Un posible diagnóstico que constituye una solución al problema diagnóstico es cualquier (mínimo) par de conjuntos de todos los nodos iniciales verdaderos y falsos tal que se cumplan las siguientes condiciones:

, el diagnóstico implica las manifestaciones observadas,

describe el estado máximo implicado por

y las observaciones, entonces

el estado máximo que proviene de un diagnóstico y las observaciones deben ser consistentes.

Según la definición anterior, se supone que un diagnóstico es mínimo, es decir, ningún par de subconjuntos de él es un diagnóstico; uno también puede considerar diagnósticos no-mínimos, o diagnósticos mínimos con respecto a un subgrafo inducido [Fuster, 1996], [Ligeza, 1996b].

A continuación se presentan ejemplos de soluciones para el problema especificado mediante un grafo presentado anteriormente. Suponer que el problema diagnóstico viene dado por , o sea, la única manifestación es verdad. En la figura siguiente se encuentran posibles grafos de la solución; los tres grafos presentados constituyen posibles soluciones para supuesto fallo. Los nodos del fondo constituyen posibles diagnósticos potenciales.

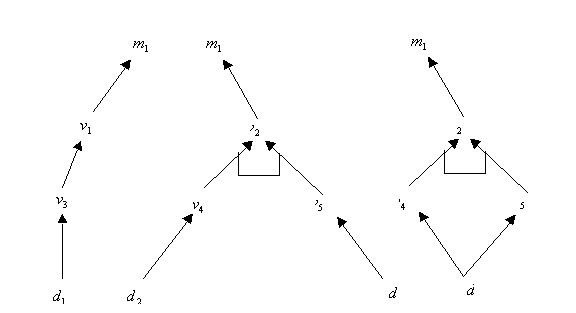
Intuitivamente hay cuatro diagnósticos mínimos, , , y ; en la figura se presentan los tres primeros.

La búsqueda de la solución se realiza por un procedimiento de búsqueda hacia atrás que selecciona e hipotetiza el estado de los nodos predecesores para explicar el estado del problema que define los nodos. Lo siguientes punto especifican las reglas de búsqueda hacia atrás usadas en el caso de las conexiones AND, OR y NO:

Nodo OR verdadero: explicado seleccionando uno de sus predecesores y volviéndolo verdadero,

Nodo AND verdadero: sólo explicado poniendo todos sus predecesores en verdadero,

Nodo OR falso: sólo explicó poniendo todos sus predecesores en falso,

Nodo AND falso: explicado seleccionando y poniendo uno de sus predecesores en falso,

Nodo NO verdadero: explicado volviendo falso su predecesor,

Nodo NO falso: explicado volviendo verdadero su predecesor,

Nodos iniciales: los nodos iniciales se vuelven verdaderos o falsos si es necesario; llegando a un nodo inicial se completa la búsqueda en el camino seleccionado.

Las operaciones sólo se realizan si no llevan a inconsistencias. El procedimiento de selección de nodos puede ser sistemático, indeterministico, o heurístico. Como el algoritmo siempre selecciona un solo nodo en el caso de nodos OR verdaderos y nodos AND falsos, las soluciones generadas son, en general, mínimas.

Con respecto a la definición, una solución al problema diagnóstico, un diagnóstico, constituye de hecho una posible explicación de los fallos observados; para verificarlo en la práctica deben probarse todos sus elementos. La validación de diagnósticos generados es el próximo paso del procedimiento diagnóstico.

Validación de diagnósticos

Con respecto al modelo de representación de conocimiento diagnóstico en forma de grafo causal AND/OR/NOT, cualquiera de los diagnósticos generados constituye una explicación suficiente del comportamiento defectuoso observado. Sin embargo, normalmente sólo uno de los diagnósticos es el válido, el problemas real en el sistema diagnosticado. De hecho, debe realizarse la validación de los candidatos obtenidos para identificar el correcto. La validación puede hacerse potencialmente mediante la simulación de la influencia de los fallos elementales supuestos en el comportamiento del sistema; sin embargo, esto requeriría un modelo más completo del sistema, cubriendo comportamientos anormales, para que puedan eliminarse todos menos uno de los diagnósticos potenciales. Esto, sin embargo, es escasamente posible en casos reales. Por lo tanto el método principal consiste principalmente en probar las causas elementales potenciales de forma directa o indirecta.

Por las razones obvias se prefieren los diagnósticos mínimos a los otros. Este punto de vista refleja la tendencia más natural a encontrar explicaciones tan simples como sea posible. principio de parsimonia. A continuación se trata el problema de validación eficaz del conjunto final de posibles diagnósticos.

Supongamos que después de una búsqueda sistemática del grafo causal se obtiene un conjunto de k posibles diagnósticos. Cualquiera de estos diagnósticos es de la forma , donde . Se supone que cualquier diagnóstico es mínimo y consistente. Si la consideración de diagnostico mínimo no es suficiente, deben considerarse todos los diagnósticos.

Una estrategia para la validación de diagnósticos puede hacerse sobre la base de varias suposiciones y de conocimiento adicional (por ejemplo uso de probabilidades y minimización de entropía). Aquí se propone una estrategia basada en un enfoque heurístico. La idea principal es separar el conjunto de diagnósticos considerados en dos conjuntos disjuntos casi iguales, como resultado de probar un síntoma que sea común en los diagnósticos.

En la parte siguiente se supone que una prueba es un procedimiento algorítmico que proporciona el valor de verdad de un solo síntoma, que es un elemento común de algunos diagnósticos. Una prueba puede confirmar un diagnóstico si el síntoma probado incluido en el mismo tiene idéntico estado a su estado en este diagnóstico; en el otro caso, la prueba rechaza el diagnóstico.

Un diagnóstico es contradictorio al diagnóstico si y sólo si o ; un elemento d que pertenezca a esta intersección será llamado elemento conflictivo con respecto los diagnósticos anteriores. Como el resultado de prueba es a priori desconocido, esta heurísticamente justificado utilizarlo: cualquiera que sea el resultado de la prueba, por lo menos uno de los diagnósticos será rechazado. La prueba "más útil" es la que rechaza el número máximo de diagnósticos al mismo tiempo. El número de diagnósticos rechazados es, sin embargo, desconocido a priori. Así, el siguiente acercamiento heurístico basado en "particiones casi iguales" queda justificado.

Sea el número de ocurrencias de d en las partes positivas de los diagnósticos , donde . Respectivamente, denota el número de ocurrencias de d en las partes negativas de los diagnósticos , donde . Así, el menor número de diagnósticos rechazado después de una prueba del elemento d, denotado con r(d), puede determinarse como

Entonces la selección propuesta de elemento(s) d para ser probado(s) debe aumentar al máximo r(d). Si denota el síntoma seleccionado para ser probado primero; debe cumplirse que:

En caso de que la selección de no sea única, pueden tenerse en cuenta otros criterios de coste heurísticos. De nuevo, teniendo suficiente conocimiento sobre probabilidades subyacentes, la prueba anterior puede generalizarse para seleccionar una prueba que rechace el máximo número esperado o medio de diagnósticos.