6.2 Estados y situaciones

¿Que es un estado?

  Al discutir los problemas de monitorización y supervisión de sistemas, uno puede preguntarse lo que va precisamente a monitorizar, supervisar y analizar. Aunque normalmente es posible observar (y a veces medir) directamente sólo la salida del sistema, la respuesta es más complicada: la objetivo principal de la mayoría de sistemas de supervisión es monitorizar y analizar el estado del sistema, incluyendo la salida como parte inherente o como caracterización externa. Entonces, la pregunta crucial a contestar es ¿que es el estado?, especialmente en los sistemas más complejo que incluyen componentes de comportamiento descritos mediante de representación de conocimiento. ¿Y cómo se representa?

En la teoría del control moderna ampliamente entendida (análisis de sistemas, modelado, simulación, diseño, y supervisión) la idea de estado físico de un sistema dinámico se usa a menudo. Según [Kwakernaak and Sivan, 1991] la idea de estado originada en la física se introdujo en la teoría del control a finales de años cincuenta. En este tiempo se ha vuelto tan popular, que algunos libros de texto modernos en control ''lo dan por entendido '' sin hacer ningun analisis, incluso superficial, de este concepto. La definición común es parecida a [Dorf and Bishop, 1995]:
 

El estado de un sistema es un conjunto de números tal que el conocimiento de estos números y la función de entrada futura, junto a las ecuaciones que describen la dinámica, proporciona el estado futuro y la salida del sistema.   La necesidad de considerar el estado como una característica tan útil en análisis de comportamiento dinámico en sistemas entrada-salida surge de la necesidad de caracterización concisa y completa de la influencia pasada en el sistema. Esta caracterización deben permitir totalmente predecir comportamiento posteriores del sistema especificando sólo la entrada.

Consideremos un sistema dinámico con entrada u(t) y salida y(t). Supongamos que estamos interesados en predecir el comportamiento de sistema y(t) para  a partir de un instante de tiempo . Por supuesto, debemos saber la función de entrada u(t) para , pero la observación y la experiencia muestran de que no sería bastante. También debemos saber u(t) para cualquier . De hecho, cuando el sistema es dinámico, puede acumular (recordar) las influencias pasadas, y esta historia acumulada puede influir en el comportamiento futuro. La historia acumulada es lo que nosotros llamamos el estado del sistema. Se requiere que los estados cubran la totalidad de influencias pasadas, para que el conocimiento de estado actual permita una única predicción del comportamiento futuro del sistema, sólo junto con el control futuro. La caracterización de la influencia pasada mediante la especificación del estado del sistema debe ser completa.

En el dominio de la teoría del control clásica, muchos autores (implícitamente) ponen por delante otro requisito: la descripción de estado debe ser mínima, es decir, ningún subconjunto apropiado de variables de estado mantiene la propiedad de ser un caracterización de estado completa. Esto parece más natural - si el estado es conocido puede calcularse cualquier otra caracterización de estado -; no hay ninguna necesidad de una representación más compleja, ya que el trato directo con esta representación más compleja puede ser problemático. Por ejemplo, si una variable de estado depende funcionalmente de otra, no cualquier combinación de variables de estado define un estado admisible. Esta dependencia funcional siempre puede agregarse a las ecuaciones de estado como restricción adicional haciendo la descripción del sistema sobre-restringida, y más difícil de tratar con la base de matemática clásica. Sin embargo, en sistemas basados en conocimiento, no debería insistirse en tener descripciones de estado es completas y especialmente mínimas: en ciertos casos puede ser más conveniente tener descripciones de estado máximas. También la descripción de estado incompleta juega un papel importante en el modelado basado en conocimiento de sistemas dinámicos (sin embargo, no necesariamente en los descritos mediante un vector de estado numérico y ecuaciones diferenciales de estado).

Otro comentario es que para muchos sistemas la representación de estado no es única. La elección de variables de estado depende de las preferencias del usuario, y normalmente no tiene influencia en los resultados del análisis, en el caso de los sistemas clásico considerados dentro de la teoría del control. En sistemas basados en conocimiento, sin embargo, la opción apropiada de representación (máxima en el peor caso) puede tener influencia en las posibilidades de comportamiento del sistema de modelado o a la hora de encontrar solución a ciertos problemas.

En [Lunze, 1994] se realiza un análisis del concepto de estado en teoría de sistemas (control automático) versus la noción de estado en AI. Con uso de un sistema de ejemplo de dos tanques, se construyen sistemas analíticos y basados en reglas como modelos para los tanques. En el modelo analítico el estado se representa por un vector de dos variables numéricas (los niveles de agua en los dos tanques). En el modelo de la base de conocimiento el estado se representa de forma cualitativa, utilizando regiones del espacio de estado original. Se especifican los límites de las regiones mediante condiciones lógicas referidas a valores umbral. El conocimiento incompleto sobre el estado del sistema (característica cualitativa) se compensa mediante el conocimiento memorizado del algoritmo de búsqueda usado para modelar el comportamiento del sistema.

El planteamiento anterior se limita principalmente a sistemas dinámicos con modelos en forma de ecuaciones diferenciales. Sin embargo, ¿qué puede decirse sobre el estado de sistemas que es imposible modelar con estas ecuaciones? ¿Qué ocurre si las características de comportamiento del sistema incluyen atributos, términos lingüísticos y relaciones? ¿Qué ocurre si el estado futuro es imprevisible?

A continuación se presenta una estructura general para la representación de estado en sistemas basados en conocimiento. Las consideraciones se basan en la asunción que la representación de conocimiento se hace mediante el uso de cálculo de predicados de primer orden o lógicas similares. En el caso de formalismo de representación de conocimiento diferentes pueden ser necesarias una interpretación apropiada y la "transfiguración" de las formulas de estado y situación.

Primero, se definen las fórmulas básicas que describen los estados del sistema. Se suponen fórmulas que describen estados que contienen toda la información acerca de los mismos, llamadas fórmulas-estado. Pasemos a la descripción parcial de estado. Una fórmula que expresa sólo parte de la información puede aplicarse a más de un estado físico, así se dice que describe un conjunto de estados, llamado situación. Esta fórmula se llamará fórmula de situación (también: contexto, familia de estados). Siguiendo la descripción de estados y situaciones, se introducen algunos funcionamientos básicos en fórmulas de situación.

Estados y fórmulas de estado

  Consideremos un sistema finito, discreto, tal que su comportamiento puede describirse mediante el uso de relaciones que especifican qué propiedades son verdad en un cierto instante de tiempo. Se tendrán en cuenta los estados físicos del sistema en instantes discretos, separados, de tiempo. Se supone, por lo tanto, que tiempo es discreto. Ahora se pueden nombrar algunas propiedades importantes de las expresiones que describen los estados físicos de un sistema.

Primero, para cualquier sistema físico realista, no es factible (es absolutamente imposible) representar toda la información acerca del estado de este sistema en un cierto instante de tiempo, sobre todo mediante el uso de expresiones finitas. Es más, teniendo en cuenta la aplicación de las expresiones de representación de conocimiento tratadas, la mayoría de la información representada se desechará, ya que será innecesaria para la tarea específica que este realizándose. Así, el formalismo de representación de conocimiento debe tener en cuenta la aplicación probable del conocimiento representado.

Destaquemos también que la representación humana del conocimiento normalmente se ajusta a algunos propósitos específicos (aplicaciones), aun cuando el sistema considerado sea el mismo. Consideremos un ordenador personal como sistema de ejemplo. Desde el punto de vista de decoración interior, características como la colocación, orientación del monitor, tamaño, forma y color serán probablemente de interés. Para el usuario del sistema, el software accesible, el tamaño de memoria, aceleración, configuración, etc., también serán de interés. Para el gerente de la empresa puede ser interesante si la computadora está operativa o averiada, cual es la eficacia media y qué clase de problemas pueden resolverse actualmente con su uso. Desde punto de vista de programación, pueden ser interesantes cosas como el número, capacidad y volúmenes actuales de los registros así como la asignación de memoria. Note que, lo que constituye una información crucial para algunos usuarios, puede ser innecesario, malgastador o incluso perturbador para los otros. Estas observaciones dan lugar a postular lo siguiente acerca de la representación de conocimiento sobre los estados del sistema.
 

Para construir un formalismo de representación de conocimiento eficaz, el conjunto de relaciones de interés debe escogerse con respecto a su probable aplicación. El grado de detalle de la descripción de estado debe depender del nivel de abstracción en el que se analiza el sistema.   Una vez escogido el nivel de abstracción y teniendo en cuenta las aplicaciones potenciales, debe poder especificarse el conjunto de relaciones de interés. Al representar el estado físico de un sistema mediante un conjunto dado de relaciones admisibles, no debe haber ningún lugar para cualquier "reticencia", toda la información de interés debe expresarse explícitamente. En caso que se pase por encima de (se salte) alguna información, la expresión resultante posiblemente puede describir más de un estado físico del sistema. Como resultado, no podrá identificarse el estado de una única manera. Así, el postulado siguiente parece estar justificado.   Una expresión que representa conocimiento sobre un estado de alguno sistema deben contener todo el conocimiento (acerca del estado) qué es posible expresar mediante el idioma y el formalismo aceptados y qué es verdad en el estado físico.   Con respecto al postulado anterior, el conocimiento acerca de un estado representado dentro del formalismo seleccionado probablemente es redundante. Esto significa que un experto del dominio (o un usuario del sistema) probablemente podrá deducir algún conocimiento a partir de sólo una representación parcial. Sin embargo, ya que para sistemas realistas parece impracticable determinar una representación mínima, es conveniente permitir el uso de representaciones quizá redundantes pero ciertamente completas. Esto es especialmente importante para el tratamiento extenso de algunas propiedades teóricas del formalismo propuesto. Sin embargo, en particular, en aplicaciones prácticas, uno es libre de "inventar" cualquier simplificación y por consiguiente representaciones más económicas, con tal de que la cantidad necesaria de conocimiento esté inmediatamente disponible si es necesario. Uno de estas simplificaciones, conocida como la suposición de mundo cerrado [Genesereth, 1987], se menciona a continuación.

Presentemos otro problema en relación con la representación de conocimiento lógica mediante un sistema que incluya el signo de negación (éste es nuestro caso). Si realmente toda la información verdadera debe estar presente en las expresiones que describen el estado, entonces toda la información que de hecho no es verdad también debe especificarse precedida por el signo de negación. Esto llevaría obviamente a expresiones torpes de poco valor práctico. En cambio, puede asumirse que sólo la información positiva se presenta explícitamente, y que cualquier cosa no declarada explícitamente puede asumirse como falsa. Éste, de hecho, es el acercamiento usado en teoría de bases de datos relacionales o sistemas de información y se aplica ampliamente en Inteligencia Artificial bajo la asunción de mundo cerrado. Lo siguiente el postulado intenta resumir esta simple observación.

  Las expresiones que representan conocimiento acerca de los estados particulares del sistema deben ser concisas, es decir, representando explícitamente sólo conocimiento positivo, con la asunción predefinida subyacente de que lo que no se declara explícitamente es de hecho negativo (o falso).   Sea P un conjunto finito de predicados (atributos, propiedades de interés), que representan las relaciones de interés. Además, se define un conjunto de constantes C (incluyendo valores de atributos y objetos). Sea S el espacio de estado de un sistema, es decir, el conjunto de todos los posibles estados (físicos) del sistema. El espacio de estado S puede ser finito, contable o infinito; por razones prácticas, en el caso de sistemas basados en conocimiento normalmente solo se consideran espacios de estados finitos (aparte de los casos donde se usan variables reales o enteras como parámetros). Para cualquier estado  se define una fórmula de estado que describe este estado con respecto a la interpretación supuesta y el conjunto de predicados seleccionados. La definición hace uso de todos los postulados especificados anteriormente.

Definición. Una fórmula de estado de algún estado  es la única fórmula simple  (en  no hay ninguna variable) que contiene todos los hechos verdaderos en este estado (sólo los positivos) posibles de expresar mediante los símbolos predicativos de P y las constantes de C.

Claramente, cualquier estado  tiene una única fórmula de estado correspondiente. Intuitivamente, una fórmula de estado correspondiente a algún estado s es una conjunción de todos los hechos que son verdad en este estado y es posible expresarlos en el idioma supuesto. Principalmente, por razones prácticas, se consideran sistemas que tienen fórmulas de estado finitas. Destaquemos también la idea de que la fórmula de estado introducida anteriormente es un tipo de noción teórica conveniente para consideraciones posteriores. En la práctica, son posibles varias realizaciones, que van desde las conjunciones simples de proposiciones (en lógica proposicional) a "teorías" definiendo el estado actual y las propiedades del sistema. Contrariamente a la automática clásica y al vector de estado, se asume que la fórmula de estado es máxima; esto se hace tanto por razones prácticas (no es una tarea trivial el encontrar representaciones mínimas para sistemas complejos y, además, no son únicas; además no hay ninguna manera fácil de compararlas y, sobre todo, para inferir todo el conocimiento que proviene de una descripción mínima) y por razones teóricas (ya que es única y contiene toda la información, esto simplifica la discusión). Sin embargo, en aplicaciones prácticas este concepto puede restringirse y modificarse.

Para clarificar las ideas anteriores consideraremos un ejemplo completo de sistema simple y una de sus posibles representaciones. Consideremos el sistema compuesto simplemente por un solo deposito con un parámetro cualitativo wl que es el nivel de agua; el atributo wl puede tomar los siguientes valores . Otro parámetro cualitativo dwl es la derivada cualitativa del nivel de agua y puede valer  dependiendo del signo de la derivada. Existe un atributo binario, system, que puede valer on o off dependiendo de si el sistema está encendido o apagado. Existen también dos fórmulas proposicionales, water_in y water_out, que valen truth si y sólo si se está vertiendo agua hacia dentro o hacia fuera. El sistema está compuesto de un tanque, una válvula de abastecimiento de agua, una válvula de salida de agua, un sensor de nivel y otro para medir la derivada del nivel. El sistema se muestra en lo siguiente diagrama de estado particular.
 



 


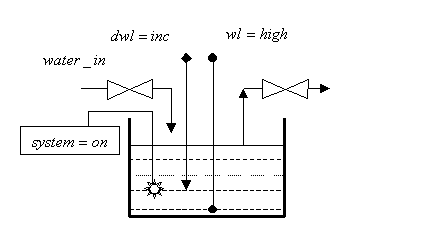
La fórmula de estado que describe el estado del sistema mostrado será:
 

Destaquemos que toda la información positiva está presente en , mientras que la información negativa, , simplemente no se da. Además, destaquemos esto con respecto a la interpretación intencional, la información en la fórmula es redundante: si el agua se está vertiendo dentro (pero no fuera), el nivel debe aumentar, pero esto se declara explícitamente en .

Hagamos algunas observaciones simples a partir del ejemplo anterior. Puede verse fácilmente, incluso dentro de la representación propuesta, que las fórmulas de estado son redundantes. Sin embargo, esto se hace a propósito. Sería difícil encontrar y guardar una representación mínima en la práctica. Además, como ya se ha mencionado, esta representación no sería única. Cualquier representación mínima también sería inoportuna por lo menos por dos razones. Primero, el sistema de razonamiento tendría que invocar un motor de inferencia específico del dominio para determinar qué otros hechos son verdad. Es más, en caso de cualquier cambio en el sistema, es probable que la representación "minima" no sea suficiente. Para ver esto imaginar que el sistema se agranda con más válvulas, etc. Si no se tiene ninguna información explícita sobre dwl, sería imposible determinarlo a partir del estado de las válvulas sabiendo sólo si algunas están cerrados y otras abiertas (tanto para anadir agua como para sacarla). La dificultad anterior proviene del hecho que nuestra deducción anterior asumió implícitamente que los recursos del sistema están limitados (que era un tipo de deducción no monotonica).

Tengamos en cuenta también que, para un sistema dado, son posibles varios idiomas de representación, aun cuando se dé el nivel de abstracción apropiado para la representación de conocimiento. Por ejemplo, en el sistema anterior pueden usarse predicados, fórmulas proposicionales o atributos binarios, etc. En general, la opción por determinados predicados dependerá de muchos factores, incluyendo características específicas del dominio, expresiones usadas habitualmente y preferencias del usuario.

Situaciones y fórmulas de la situación

  En la subsección precedente se ha introducido un método formal para la representación de estados. A grandes rasgos, el método consiste en listar todos los hechos que son verdad en un estado dado, con la asunción que los hechos negativos (qué son verdad, ya que sus negaciones son falsas) no se especifican explícitamente, sólo para ser concisos. Además, en algún sistema específico, puede ser posible construir infinitamente muchos hechos que no son verdad, y así las fórmulas de estado serían de longitud infinita.

Como en el ejemplo mostrado anteriormente, en algunos sistemas simples pueden usarse fórmulas de estado para describir los estados del sistema completamente, (como se ha declarado por definición). Sin embargo, en el caso de sistemas más complejos el uso de fórmulas de estado completas puede no ser factible, simplemente debido a su longitud. Además, probablemente no toda la información dada por una fórmula de estado será de interés primordial en cualquier instante de tiempo. Aún más, en ciertos casos sólo puede estar disponible información incompleta. Esto da lugar al uso de una especificación parcial del conocimiento que involucran los estados físicos.

Existe también otro propósito en el uso de especificaciones de conocimiento incompletas. Estas especificaciones proporcionan condiciones de hecho más débiles acerca del estado descrito, y como tales pueden aplicarse a más de un estado físico. Así, pueden usarse estas características técnicas incompletas para describir conjuntos de estados.

Sea S un espacio de estado de un sistema. Cualquier conjunto se llamará situación. Como antes, P denota un conjunto finito de predicados seleccionados que representan las relaciones de interés que involucra el sistema, y S es el espacio de estado del sistema. Para cualquier subconjunto  se define una fórmula de la situación que describe todos los estados de la situación y sólo ellos, con respecto a la interpretación supuesta y al conjunto de predicados seleccionados.

Definición. Una fórmula de situación de una situación , es cualquier fórmula  más general que cualquier fórmula de estado para el estado , es decir,  para  (donde  es una fórmula del estado ), y simultáneamente  no generaliza ninguna otra fórmula de estado.

Con respecto a la definición anterior, una fórmula de situación es cualquier fórmula más general que cualquier fórmula de estado de cualquier estado que pertenezca a esta situación, pero, simultáneamente, tal que no generaliza ninguna otra fórmula de estado. Note que, cualquier fórmula del estado es de hecho una fórmula de situación para una situación que sólo consiste en este estado (una situación de un solo elemento). Puede observarse que dos fórmulas del estado son incomparables con respecto a la generalización, es decir, ninguna de ellas puede ser más general que la otra. Si uno de ellas fuera más general que la otra, sería una fórmula de la situación automáticamente, ignoraría la condición de especificación de conocimiento completo. Puede observarse que cualquier fórmula es una fórmula de situación para alguna situación (posiblemente una situación vacía). También es importante que, dentro de un idioma, es posible crear una fórmula de situación para cualquier situación. Esta posibilidad se asegura porque la fórmula puede tomar la forma de disyunción de fórmulas de estado de todos y sólo de los estados que pertenecen a la situación. Sin embargo, no es cierto que cada situación pueda ser representada por una fórmula conjunta simple. No hay en general, es más, ni una-a-una correspondencia entre las situaciones y fórmulas de situación. Para una situación dada puede existir más de una fórmula de situación.

La aplicación principal de fórmulas de situación incluye representación parcial de estados del sistema y, sobre todo, la especificación de condiciones, restricciones, requisitos, etc., especificando algunos grupos de estados de interés, como alarmas o situaciones peligrosas, condiciones previas de reglas, etc. Por ejemplo, una fórmula de situación  especifica todos los estados potencialmente peligrosos que pueden ocurrir antes de un desbordamiento. Como para el estado del ejemplo, este estado puede ser considerado como peligroso, y en esta situación se genera una alarma.