6.1 De los datos al conocimiento

Pasos básicos desde los datos al conocimiento

  Contrariamente a los datos típicamente representados por una gran cantidad de ítems de estructura simple uniformemente representados (típicamente una inmensa colección de ellos), cada uno de ellos teniendo separadamente cierto valor con poca información, puede considerarse el conocimiento como un conjunto de expresiones con estructura interna, cada uno de las cuales esta relacionada con las otras de alguna manera, y conteniendo cantidades relativamente grandes de información comparativamente a su tamaño. Los datos son normalmente extensos y redundantes. Representan extensionalmente y explícitamente algunos fenómenos de interés y sus propiedades. El conocimiento, por otro lado, es mucho más conciso, intensivo, y raramente redundante (la redundancia de conocimiento puede ser considerada como un problema; incluso las bases de datos relacionales se planifican normalmente para evitar redundancia). Los fenómenos de interés se caracterizan de forma intensiva e implícita mediante el conocimiento formalmente especificado.

Para preparar el conocimiento de entrada de los sistemas de supervisión basados en conocimiento, la gran cantidad inicial de datos debe transformarse a una forma de conocimiento más concisa y significativa. Las siguientes actividades constituyen las operaciones básicas para pasar del nivel de los datos al nivel del conocimiento, del nivel de la información numérica extensa al nivel semántico, simbólico, cualitativo y conciso del conocimiento:
 

  • Preselección de datos numéricos pertinentes y necesarios; los datos innecesarios simplemente se descartan o se rechazan,
  • Fusión de datos (de varias fuentes diferentes a una sola fuente),
  • Abstracción del datos y generalización, generando objetos más abstractos (por ejemplo valores cualitativos), encontrando sus propiedades y descripciones generales,
  • Simbolizacion, generación de conocimiento codificado simbólicamente, normalmente encontrando las relaciones entre el objeto abstraído y estados,
  • Análisis posterior, refinamiento y comprobación de propiedades del conocimiento generado.
    •


    Aunque no siempre se aplican todas las operaciones, pueden considerarse como básicas, pasos genéricos, constituyendo un posible procedimiento de transformación de datos-en-conocimiento. Aquí se presentan en el ámbito abstracto, independientemente del dominio y las herramientas; para su aplicación práctica, las operaciones particulares deben traducirse y codificarse de forma específica según el formalismo de representación de conocimiento, los datos adquiridos y el nivel de abstracción.

    Abstracción y generalización

      Presentemos un poco mas formalmente las ideas de abstracción y generalización, como aplicaciones en el dominio del procesado de datos y conocimiento. La abstracción se significa principalmente por ser el proceso de pasar de una representación detallada orientada a datos a otra orientada a conocimiento de nivel superior. La abstracción se logra a través de ciertas operaciones específicas en los datos, principalmente borrar ciertos ítems y fusionar otros. La Generalización es la relación del conocimiento más abstracto con el más detallado, una relación entre dos ítems de representación de conocimiento (fórmulas). El conocimiento más general se obtiene como resultado de operaciones de abstracción realizadas en los datos iniciales. Así, la abstracción puede percibirse como una operación que lleva a la generación de una representación de conocimiento más general, describiendo una clase más amplia de ítems que anteriormente. El concepto formalmente introducido de generalización permite manejar ideas algo intuitivas acerca de la abstracción de datos.

    Las nociones presentadas involucran representación de conocimiento y se refieren a la comparación de expresiones de representación de conocimiento diferentes con respecto a los conjuntos de objetos que satisfacen las descripciones. Se involucra la interpretación de formulas con respecto a algún universo de discurso y, simultáneamente, la comparación de ellas con respecto a su alcance y a la exactitud del conocimiento representado. A grandes rasgos, se define y se analiza una relación de orden con respecto a la ‘cantidad de información’ representada por una fórmula.

    La misma idea de noción presentada de generalización consiste en la interpretacion de formulas lógicas o cualquier otra expresión de representación de conocimiento en términos de conjuntos de objetos descritos (normalmente estados del universo de discurso) en lugar de considerar las formulas como los axiomas y teoremas de algunos sistemas formalizados. Consideremos dos formulas u otras expresiones de representación de conocimiento  y . Se considera que las dos expresiones anteriores describen sistemas dinámicos (universos, mundos). Así, a cualquiera de las expresiones puede asociársele un conjunto físico de estados para los que la fórmula es válida. A grandes rasgos, cuanto más grande es el conjunto más general se considera la fórmula adjunta. Una fórmula generaliza otra fórmula si describe un conjunto más grande de estados con respecto al universo de discurso. Más formalmente, sean  y  los conjuntos de estados u otros ítems descritos por las correspondientes formulas. Se dice que  es más general que, , si y sólo si . Intuitivamente, la idea de generalización se presenta de forma gráfica en la siguiente figura.
     

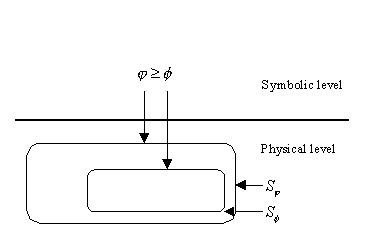
    La relación presentada es válida en el conjunto de todas las formulas lógicas de primer orden. De hecho,  si y sólo si  Æ, la fórmula más detallada conlleva lógicamente la más general. Más adelante se presentan esquemas de verificación basados en modos de inferencia específicos para formulas simples y normales. En secciones posteriores se discuten las aplicaciones en sistemas dinámicos basados en conocimiento. La idea principal del concepto propuesto de interpretación lógica puede explicarse más precisamente.

    Destaquemos que, a grandes rasgos, si una fórmula contiene información detallada (muchos hechos, por ejemplo), entonces el conjunto correspondiente de estados es bastante pequeño, ya que toda la información debe ser verdad en cualquiera de los estados. Al contrario, si una fórmula contiene información parcial (sólo varios hechos), puede realmente describir un conjunto numeroso de estados, ya que el requisito de información verdadera en cualquiera de los estados es bastante débil. Puede decirse directamente que una fórmula más general describe más estados que una menos general.

    Para proporcionar algunas intuiciones acerca de la noción de generalización pueden mostrarse las maneras básicas de hacer más general a una fórmula, de resumir la información Éstas son:
     

  • Eliminando una condición (e.g. un literal) en cualquier fórmula conjuntiva,
  • Agregando una posibilidad extra en una fórmula disyuntiva,
  • Convirtiendo una constante en una variable (implícitamente existencialmente cuantificada).
    •


    Examinemos las posibilidades anteriores de una manera más detallada. Sean  y  fórmulas lógicas; entonces:
     


    ,


     


    eliminando una condición en cualquier fórmula conjunta se hace más general. Igualmente:

    ,


     


    agregando una fórmula (disyuntiva) se hace más general. La tercera posibilidad consiste en reemplazar una constante (o un término) por una variable y aplica a lógica de predicados o un calculo similar.

    ,


     


    donde X es una variable reemplazando alguna constante a. Otras posibilidades incluyen extensiones de un solo valor o conjunto a un conjunto más grande o intervalos cerrados.

    Las tres vías de generalizar una fórmula constituyen las posibilidades más básicas y naturales. Otra posibilidad proviene de los métodos de inferencia lógica.

    Se definirá una relación de la equivalencia con respecto al grado de generalidad como sigue. Dos fórmulas  y  se dice que son igualmente generales () si y sólo si  y . Intuitivamente, dos fórmulas igualmente generales tienen el mismo "poder expresivo", describen el mismo conjunto de estados del mundo o sistema considerado. Puede demostrarse que la relación de generalidad es igual a una relación de equivalencia (es reflexiva, simétrica y transitiva) mientras que la relación del generalización es una relación del orden parcial (es reflexiva, antisimétrica y transitiva).

    La definición presentada de generalización no proporciona ningún método constructivo para verificar si una fórmula dada es más general que otra fórmula - verificar si una fórmula proviene lógicamente de otra es, en general, un problema de cálculo muy complejo. Sin embargo, en muchos casos, puede observarse que, gracias a la forma simple y regular de las fórmulas positivas simples conjuntivas, es posible verificar si la generalización se cumple mediante el simple análisis de las dos fórmulas. Se ha presentado la manera de verificar generalización para el formalismo lógico y la representación de conocimiento atributiva.

    Problemas en la adquisición de datos

      Consideremos la representación tabular de datos, donde los datos están en tablas como en bases de datos correlativas; esta forma de representación de datos también puede considerarse igual a la representación atributiva. Esta representación es popular y ampliamente aceptada. Es entendida fácilmente por los expertos y, además, pueden aplicarse el motor y todas las nociones bien establecidas de las bases de datos correlacionales. A continuación, se intentaran tratar los problemas acerca de la adquisición de información que usa la forma tabular y las nociones básicas del dominio de las bases de datos. Una ventaja de este enfoque consiste en la posibilidad de aplicar operaciones normales de bases de datos en algunos pasos del preprocesado. Los problemas con los datos de entrada pueden ser clasificados según el esquema siguiente, escueto pero comprensible:
     
  • Sobrecarga de datos, demasiados datos. Este caso normalmente es resultado de capturar diferentes tipos de datos sin un plan específico de su uso. El problema es que no todos los datos son pertinentes a los problemas considerados, y su procesado consume tiempo. Además, ocupan innecesariamente mucha capacidad de almacenamiento. Pero el problema más importante es que cuando se proporciona a un operador humano tal cantidad de datos puede causar ''sobrecarga cognitiva'' y crear dificultades de percepción, comprensión y decisiones erróneas. Lo mismo puede suceder para un sistema de supervisión basado en conocimiento, incapaz de tratar con datos abundantes. A continuación se tratan algunos aspectos específicos de la sobrecarga de datos y algunas maneras básicas de tratarla:
    •