Representación de conocimiento mediante Lógica Proposicional

Repasemos las bases de la lógica proposicional. Una proposición es una sentencia finita a la que puede asignarse un valor de verdad: verdadero o falso. El alfabeto del cálculo proposicional consiste en un conjunto (infinito) de símbolos proposicionales, normalmente denotados como , etc., y un conjunto de conectivas lógicas. Los símbolos proposicionales también se llaman fórmulas atómicas, o átomos (para abreviar). Como conectivas lógicas usadas frecuentemente encontramos  (negación; no),  (conjunción; y),  (disyunción; o),  (implicación; si... entonces...), y  (equivalencia; si y sólo si). Algunas veces también se usan conectivas especiales, pero todas las funciones especiales pueden expresarse como combinaciones apropiadas de las anteriores. Más precisamente, cualquier conjunto mínimo pero funcionalmente completo de conectivas lógico es suficiente para expresar cualquier función lógica en cálculo proposicional. Ejemplos de tales conjuntos mínimos pero funcionalmente completos son o , mientras que la conjunción y la disyunción no forman ningún conjunto funcionalmente completo. La razón de usar más de un conjunto mínimo funcionalmente completo de conectivas es la tradición y la simplificación a la hora de crear funciones más complejas. Es más, el uso de más funciones y paréntesis mejora la legibilidad. Las fórmulas de lógica proposicional se definen inductivamente como sigue:
 

Cualquier símbolo proposicional p es una fórmula,

Si  y  son fórmulas, entonces, , ,  y 

también son fórmulas.

Nada más es una fórmula. A veces, se usan paréntesis para establecer prioridades de operadores lógicos; si no aparece ningún paréntesis en una fórmula (subformula), entonces normalmente las prioridades disminuyen de la negación a la equivalencia en el orden mostrado.

La semántica de cálculo de predicados es también bastante simple. La evaluación del llamado valor de verdad de una fórmula puede realizarse en cuanto las fórmulas proposicional sean individualmente verdaderas o falsas. Para simplificar, los dos valores de verdad se denotan también con 1 y 0, V y F, etc. Una forma práctica de evaluar el valor de verdad de fórmulas más complejas se define mediante la siguiente tabla:
 

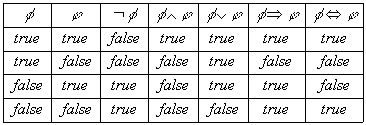
Si una fórmula se evalúa como verdadera bajo cierta asignación de valores de verdad a los símbolos proposicionales, se dice que la fórmula se satisface bajo esta asignación (interpretación). Una fórmula verdadera bajo cualquier asignación se llama válida o tautología. Una fórmula que siempre se evalúa como falsa, independientemente de la asignación de sus proposiciones sele llama "unsatisfiable". Si existe al menos una asignación tal que la fórmula sea satisfecha, se le llama "satisfiable". Para evaluar el valor de verdad de cualquier fórmula deben aplicarse las reglas de la tabla inductivamente, hasta generar la evaluación de la fórmula total.

Para denotar el hecho que alguna fórmula  siempre es verdad (tautología) se usa la siguiente notación: Æ. Por ejemplo, , o sea Æ. Otro ejemplo de tautología es . Aún más, consideremos dos fórmulas y  (quizás con algunos símbolos proposicionales comunes). Si cualquier asignación que satisface también satisface  entonces este hecho se denota como  Æ y se dice que conlleva o que  es una consecuencia lógica de . Por ejemplo, Æ para  y .

El cálculo proposicional puede usarse para construir modelos, sobre todo para sistemas en los que los elementos exhiban dos estados estables distinguidos (elementos bi-estables). Estos elementos incluyen cualquier sistema mecánico, eléctrico, hidráulico o neumático, etc. sistemas de relés, circuitos digitales, y sistemas similares. También pueden codificarse mediante símbolos proposicionales otros sistemas de naturaleza más compleja, en los que su comportamiento se resume a síntomas observados.

Agregando potencia expresiva: elementos del cálculo de predicados

El alfabeto de lógica de primer orden consiste en símbolos que denotan objetos (constantes), funciones y relaciones, conectivas lógicas, cuantificadores y elementos auxiliares, como los paréntesis y comas. Las constantes denotan objetos específicos, valores, o fenómenos. Las variables se usan para denotar los mismos elementos en el caso de que el nombre preciso de un elemento no se conozca, sea irrelevante o deba representarse una clase de elementos. Simultáneamente, las variables juegan el papel de restricciones, dos o más ocurrencias de la misma variable en una expresión denotan el mismo objeto; si se da cualquier reemplazo de variables, deben reemplazarse todas las ocurrencias de la misma variable por el mismo símbolo. Los símbolos de la función denotan, en general, mapas; sin embargo, pueden aplicarse para formar estructuras tipo registro para representar objetos más complejos. En este caso, puede asumirse que una función mapea sus argumentos en el objeto estructurado resultante. Para especificar relaciones que se mantienen en los objetos con toda seguridad se usan símbolos de predicado. Las relaciones representadas pueden no tener ningún argumento (y así ser iguales a los símbolos proposicionales descritos anteriormente) o pueden tener uno o más. Intuitivamente, el significado es que la relación se cumple para los argumentos especificados.

En la notación presentada, las variables se denotan con caracteres o cadenas, siempre empezando por una letra mayúscula o subrayada, Las constantes se denotan con cualquier otra cadena de caracteres y símbolos especiales o letras solas (típicamente una sucesión de letras minúsculas y posiblemente caracteres subrayados; esta convención se usa para mejorar la legibilidad). Las funciones y predicados se denotan con cualquier carácter arbitrario o cadena; son fácilmente reconocibles por su posición en cualquier expresión. Se usan frecuentemente nombres propios para proporcionar algunas intuiciones y referirse manualmente a algunos ejemplos específicos. Si es necesario, algunas veces se usan índices para proporcionar definiciones relativamente precisas y teoremas.

Cualquier función y símbolo de predicado toman un número de argumentos especificado previamente. Si para algún símbolo de función f (símbolo de predicado p) el número de argumentos es n, el símbolo apropiado se llama el lugar n o n-esimo símbolo de función (predicado). El número de argumentos de cualquier función o predicado (su paridad) puede ser cero o cualquier entero positivo; sin embargo, por convención, todas las funciones de lugar 0 se consideran como constantes.

Las conectivas lógicas usadas están, en principio, limitadas al igual que en el caso del cálculo proposicional ( (negación; no),  (conjunción; y),  (disyunción; o),  (implicación; si... entonces...), y  (equivalencia; si y sólo si)). También puede usarse los cuantificadores lógicos  (cuantificador universal) y  (cuantificador existencial). Todas las conectivas lógicas y cuantificadores pueden usarse para construir expresiones lógicas más complejas, o sea fórmulas.

Para representar cualquier objeto en lógica de predicados es necesaria la noción de término. Un término es cualquier constante, variable o expresión de la forma , donde f es un símbolo funcional n-ario y  son términos; la definición es, entonces, inductiva. Por ejemplo, las siguientes expresiones son términos bien construidos on, off, input_1, output_3, switch(input_1,output_1,output_2), distance(state,goal), etc. El significado preciso de un término debe estar siempre definido en un contexto particular asignándole una interpretación intencional. Los símbolos funcionales y constantes se seleccionan de forma que simplifiquen la interpretación.

Las fórmulas básicas de lógica de predicados son fórmulas atómicas (átomos, para abreviar). Una fórmula atómica siempre tiene la forma , donde p es una relación de n argumentos y  son términos. Las fórmulas atómicas en lógica de predicados corresponden a átomos de cálculo proposicional. La asignación de verdad a fórmulas atómicas se realiza básicamente verificando si la relación especificada p se cumple para los objetos definidos por los términos. Algunos ejemplos de fórmulas atómicas pueden ser

holds(signal, on),
status(switch_1,off), o
connected(input_1,switch(input_1,output_1,output_2),output_2).

Las fórmulas atómicas positivas en las que no se encuentra ninguna variable son llamadas normalmente hechos.

Las fórmulas más complejas se forman a partir de las atómicas casi exactamente como en el caso del cálculo proposicional. La única diferencia consiste en el uso de cuantificadores. Si una variable se encuentra en una fórmula atómica, entonces se llama variable libre. Esta variable no tiene ningún significando definido y seria difícil asignarle algún valor de verdad a este átomo. El uso de cuantificadores permite definir "el significando" de esta variable; si una variable se encuentra dentro del alcance de un cuantificador, entonces se llama limitada. En ciertos casos, los cuantificadores no se especifican explícitamente; en estos casos se asumen que todas las variables de interés estan, implícitamente, existencialmente o universalmente cuantificadas. La convención más típica en demostración automatizada de teoremas (método de resolución) en un lenguaje de programación lógico (Prolog) es que todas las variables se cuantifican universalmente (por defecto). En ciertos casos, como en la especificación incompleta del estado de algún sistema, pueden cuantificarse ciertas variables existencialmente de forma implícita.

En muchos casos, las variables que se encuentran en una expresión lógica hacen el papel de parámetros a ser reemplazados por los valores actuales. Este reemplazo de variables por términos se llama instanciación o, más frecuentemente, substitución. Una substitución es cualquier mapeo finito de variables en términos. Una substitución puede representarse convenientemente como un conjunto de pares variable/termino y especificar, de este modo, explícitamente qué términos se sustituyen para qué variables. Una forma genérica de substitución es . Esta substitución define que las variables  son reemplazadas simultáneamente por los términos . Normalmente se supone que  (para evitar substituciones vacías) y que  no se encuentra en el término  (para evitar problemas de substituciones recursivas). Por ejemplo, si es una fórmula atómica y  es una substitución, el resultado de aplicar  a se denota como , y obviamente.

Algunas de las fórmulas más útiles son de nuevo fórmulas simples, conjunciones de fórmulas atómicas positivas (no negativas). Estas permiten la especificación de algunas propiedades que se cumplen simultáneamente. Por ejemplo, la fórmula puede especificar un estado en el que switch_1 esta abierto, la temperatura de refrigeración es normal y la velocidad es baja.

Considerando dos fórmulas arbitrarias de lógica de predicados,  y , puede ser bastante difícil verificar si  Æ, es decir, si una de ellas sigue lógicamente de la otra. Este chequeo es sin embargo muy frecuente en aplicaciones prácticas. Por ejemplo, para verificar si se cumplen ciertas condiciones en el estado actual o si se satisfacen las condiciones previas de una regla de la inferencia. Sin embargo, si se restringen las fórmulas a las fórmulas simples positivos, el chequeo puede simplificarse un poco. Esto se declara en la siguiente proposición.

Proposición. Consideremos dos fórmulas simples positivos,  y . La fórmula  sigue lógicamente de la fórmula  (la fórmula  conlleva la fórmula ) si y sólo si existe una substitución , tal que para cualquier hecho de la fórmula  existe algún hecho  en la fórmula , tal que ; (en otras palabras, ); esto se denota como  Æ, y se llama substitución "match".

Puede verse que la noción de suposición lógica en formalismo lógico corresponde de hecho a la noción de generalización en formalismos de representación de conocimiento atributivos o similares.