4.4 Representación cualitativa del conocimiento   La representación cualitativa del conocimiento se refiere a ítems no numéricos pero que muestran algún orden y, quizás, propiedades aritméticas. Esta sección perfila los acercamientos básicos a las representaciones cualitativas usadas en AI para el modelado, el control, la supervisión y el diagnóstico de procesos.

Necesidades de la representación cualitativa del conocimiento

  Una de las áreas de investigación más interesantes actualmente en Inteligencia Artificial (IA) es el campo del desarrollo, análisis y aplicación de métodos de cálculo simbólicos para la representación de conocimiento y el razonamiento sobre el comportamiento de sistemas dinámicos complejos. Las líneas de investigación más intensas incluyen el modelado y simulación del comportamiento de sistemas, el análisis de sistemas y el diagnóstico de comportamientos anormales.

A pesar del éxito indiscutible de los métodos analíticos clásicos basados en la matemática clásica (ecuaciones diferenciales o en diferencias), hay todavía una necesidad de acercamientos y herramientas para tratar con sistemas complejos, normalmente descritos a nivel lingüístico. Especialmente importante es el caso del conocimiento impreciso e incompleto. En estos casos, las aproximaciones de la IA basadas en la observación del comportamiento humano y la heurística son candidatas a ser soluciones potenciales.

Hay varios formalismos particulares para el razonamiento cualitativo sobre sistemas dinámicos. Una revisión de las tendencias actuales de investigación puede encontrarse en [Dague, 1995]. En el capitulo 6 se trataran muy brevemente algunos de estos formalismos.

En lo siguiente subsección se perfila el formalismo de Kuipers [Kuipers, 1986], uno de los más populares y el matemáticamente más elegante En cierto sentido, este formalismo es una extensión de otros formalismos que usan sólo el álgebra de signos (el espacio cualitativo se limita a tres elementos, {-,0,+}). La extensión principal aquí consiste en admitir la división del espacio cualitativo en un número arbitrario de intervalos definiendo los llamados hitos. Como simulación, puede considerarse como un enfoque especializado basado en reglas. Además, otra de las características importantes de este enfoque es el uso de restricciones, que permiten la reducción del número de predicciones de comportamiento.

Primero, sin embargo, se empezara con la presentación de algunos problemas básicos de cálculo impreciso basados en el cálculo intervalar. A continuación se presentarán los fundamentos matemáticos de la representación cualitativa de conocimiento y se revisaran sus aplicaciones potenciales.

Problemas de cálculo intervalar

  En el caso de conocimiento impreciso sobre determinados sistemas, la idea más obvia es considerar sus parámetros como especificados con alguna exactitud. Desde el punto de vista matemático, en lugar de un valor preciso, x, se admite un intervalo , tal que . Las reglas básicas de cálculo del intervalo son:
 
  • adición: ,
  • substracción: 
  • multiplicación: 
  • división: , con tal que 
    •


    El problema básico del cálculo intervalar es el aumento de imprecisión al desarrollar los cálculos. Para remarcar esto, consideremos la suma de n intervalos idénticos  , donde . Como resultado se obtendrá el intervalo , si la exactitud del parámetro inicial  fuera , la exactitud del resultado es igual a ; a grandes rasgos, esto significa que el resultado es n veces menos preciso. En el caso de sistemas dinámicos donde el próximo estado se calcula iterativamente a partir del actual, después de varios pasos de simulación la descripción del estado puede volverse arbitrariamente imprecisa. Esto puede cuestionar la utilidad de este tipo de simulación.

    La característica importante básica del enfoque de Kuipers con respecto al basado en intervalos es que la exactitud de la simulación se mantiene dentro del espacio cualitativo inicial (en algunos casos pueden detectarse nuevos hitos). Desgraciadamente, el comportamiento predicho no es único (a pesar de algunos casos simples); además, pueden generarse las llamadas falsas predicciones de comportamiento.

    La representación cualitativa del conocimiento basada en hitos

      A continuación se presentará el formalismo matemático básico que sostiene uno de las aproximaciones más interesantes, generales y significativas del modelado y simulación cualitativos. Esta aproximación fue propuesta por Kuipers en [Kuipers, 1986]. Una ventaja importante de este formalismo es que es cercano a la teoría de control y, en casos de conocimiento incompleto, puede aplicarse para la predicción cualitativa de comportamientos dinámicos.

    Como en teoría de control, se supone que el comportamiento de un sistema dinámico se caracteriza a través de varios parámetros reales. Los valores exactos de estos parámetros varían en el tiempo. Este conjunto de valores (a veces considerado como mínimo) en un cierto instante de tiempo constituye el llamado vector de estado. El conjunto de todo los valores del vector de estado a lo largo del tiempo constituye la trayectoria del sistema o historia.

    Se asume que cualquier parámetro físico del sistema considerado es una función de la forma:
     

    donde  es la recta real extendida. Se asumen que el dominio y el recorrido de f son intervalos cerrados incluidos en .

    A partir de aquí se supone que cualquier función f considerada es una función llamada razonable, o sea, continua en su dominio (), continuamente diferenciable en , que sólo tiene un numero finito de puntos críticos en cualquier intervalo limitado, y que la primera derivada es continua por la derecha en a y por la izquierda en b. El primero y el segundo puntos constituyen el requisito que f deben ser suficientemente regular, o sea, continua y suave. El tercero excluye las funciones cuyo comportamiento cambia infinitamente rápido alrededor de algunos puntos. El cuarto requisito es necesario para excluir comportamientos anormales alrededor del los limites del intervalo del dominio.

    Para definir el comportamiento cualitativo de una función razonable se le asignan un conjunto de valores característicos, llamado hitos. Cada función razonable  tiene asociados un conjunto de hios. Se supone que los hitos incluyen 0, f(a), f(b), y el valor de f(t) para cualquier punto crítico; también pueden incluir cualquier número de valores adicionales.

    Además, se distinguen los instantes de tiempo asociados a los hitos;  es un punto de tiempo distinguido de f de si t es el límite de algún subintervalo de  para que el f es igual a algún hito. Intuitivamente, los puntos de tiempo distinguidos describen los instantes de tiempo en los que ocurre algo importante, por ejemplo cruzar un hito o alcanzar un extremo.

    Una función razonable tiene un conjunto finito de puntos de tiempo distinguidos:
     

    y un conjunto finito de hitos:
      Para el resto de consideraciones una asunción básica es que sólo pueden describirse los comportamientos cualitativos de un sistema mediante el uso de hitos y el signo de la primera derivada, o sea, los valores precisos de f se reemplazan por un conjunto de puntos e intervalos; de esta forma se introduce una representación cualitativa más abstracta. Para cualquier , se define como estado cualitativo de f en t, donde  se define como: y Así, el estado cualitativo de un sistema de un solo parámetro se describe mediante el valor cualitativo de este parámetro, que es un hito o un intervalo, y el signo de su primera derivado que indica la dirección de cambio. El estado cualitativo definido de esta forma permanece estable entre cualquier par de puntos de tiempo distinguidos; esto es así porque qval se mantiene entre dos hitos vecinos (o permanece estable en el mismo valor del hito) y su derivada cualitativa no puede cambiar su valor entre el puntos de tiempo distinguidos vecinos. Así pues, para puntos de tiempo adyacentes  y  puede definirse el estado cualitativo  en el intervalo  como simplemente  para cualquier . El comportamiento cualitativo de f en  es por consiguiente la sucesión de sus estados cualitativos:
      Además, puede definirse el estado cualitativo para un conjunto de funciones razonables de la siguiente manera. Sea  un conjunto de funciones razonables, donde . El conjunto de puntos de tiempo distinguidos de F es la unión de los conjuntos de punto de tiempo distinguidos de todas las funciones individuales; cualquier función  puede tener su propio conjunto de hitos. El estado cualitativo de un sistema F de m funciones es el conjunto de los m estados cualitativos de las funciones individuales:
     


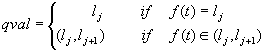
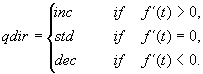
    El comportamiento cualitativo de F es la sucesión apropiada de estados cualitativos:
     

    Esta sucesión es la trayectoria cualitativa del sistema. Cualquier estado de un sistema dinámicos caracterizado por un conjunto de funciones razonables que representan los cambios de sus parámetros con el tiempo tiene una descripción cualitativa precisamente definida, QS(F,t). Puesto que la representación cualitativa sólo cambia en un numero finito de puntos de tiempo distinguidos discreto y permanece constante en intervalos abiertos entre ellos, podemos entender como ''siguiente estado'' el siguiente estado cualitativo distinto del sistema.

    En monitorización y supervisión de sistemas dinámicos, el problema básico es la representación de estado. Usando los formalismos presentados, el estado de un sistema dinámico F compuesto de m funciones (variables de estado) puede representarse prácticamente como se expone a continuación. Seleccionemos m atributos , , tales que el i-esimo atributo es justo el valor cualitativo qval de la i-esima función (puede ser un hito o un intervalo entre dos hitos adyacentes). Además, seleccionamos otro conjunto de m atributos , , interpretando cada uno de ellos como el valor cualitativo de la primera derivada qdir de la respectiva función; su valor sólo puede ser inc, std, o dec, dependiendo de si la función está aumentando, se mantiene o disminuye, respectivamente. Sea t cualquier instante de tiempo. Usando la representación atributiva de conocimiento, una fórmula conjuntiva simple que representa el estado cualitativo del sistema (parametrizado mediante t) puede representarse como:
     

    Intuitivamente, es conveniente imaginar cualquier estado cualitativo como un pequeño hipercubo cuyas dimensiones están definidas por los valores  (expresados mediante hitos) junto a un vector  asignado a él. Una fórmula más general, correspondiente a "agrandar" el hipercubo extendiendo los límites de cierta dimensión (cualquier par de hitos, no sólo adyacentes) y/o admitiendo más de un valor de para algun  corresponderá a una situación cualitativa y cubrirá varios estados cualitativos. Intuitivamente, corresponderá a un hipercubo más grande con, hablando a grandes rasgos, menos precisión en el vector de valores y derivadas cualitativos.