4.11 Grafos y grafos causales
Dependiendo de la aplicación particular, varias modificaciones de la definición básica son posibles. Generalmente, pueden admitirse varios tipos diferentes de nodos y varios tipos diferentes de uniones entre ellos. Algunas uniones pueden tomar formas funcionales más complejas, pudiendo unir varios nodos de entrada y varios nodos de salida. Son posibles varias interpretaciones de los nodos y de las uniones.
Esta sección esta dedicada a la presentación de una selección básica de modelos basados en grafos, con especial atención a aquellos modelos que incorporan grafos causales. Existen diversas aproximaciones basadas en la noción intuitiva de causalidad y en la representación gráfica de dependencias causales entre síntomas (eventos, variables, nodos). Algunas de estas representaciones más típicas se esbozan a continuación. En el Capítulo 7 se presentará un modelo más general basado en grafos causales lógicos.
Arboles de fallos
Un árbol de fallos consiste en nodos que representan eventos
en y puertas logicas, normalmente AND y OR, para representar las relaciones
entre eventos. Típicamente, pueden distinguirse cuatro tipos de
eventos:
Los eventos se conectan mediante flechas de unión; un nodo
OR representa la disyunción de condiciones que causan una salida,
mientras un nodo AND representa la conjunción de condiciones que
causan la salida. Un ejemplo simple de árbol de fallos se presenta
en la siguiente figura.
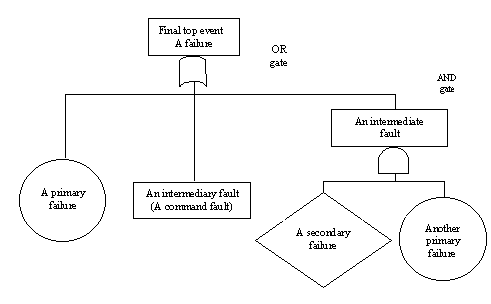
Otro ejemplo de árbol de fallos puede encontrarse en [Barlow and Lambert, 1975], donde se describen su construcción y su uso En [Isermann, 1994] pueden encontrarse ejemplos mas complejos, incluyendo razonamiento difuso para la evaluación de los fallos.
El modelo de árbol de [Barlow and Lambert, 1975] puede usarse de varias maneras para analizar la seguridad de sistemas. Las posibles aproximaciones incluyen simulación de fallos, análisis de propagación de fallos, asignación probabilística de seguridad e inferencia de diagnóstico. A continuación se presenta un algoritmo útil para la identificación de posibles causas de funcionamiento defectuoso observadas del sistema. El procedimiento se llama minimum cut set algorithm.
Un cut set es un conjunto de eventos básicos tal que la ocurrencia simultánea de estos eventos causa el evento superior. Un cut set es mínimo si ningún subconjunto puede causar el evento superior. Para un solo evento superior puede haber varios cut set mínimos diferentes. Una lista de todos los cut set mínimos - si es posible - puede ser útil para analizar la seguridad, identificando posibles o potenciales causas de fallo y - posiblemente - rediseñando el sistema para lograr nivel apropiado de seguridad.
El principio básico del algoritmo consiste en el análisis
hacia atrás de las causas potenciales de un evento seleccionado.
A destacar que, en el caso de puertas OR hay varias causas alternativas,
mientras en caso de puertas AND hay una sola causa pero compuesta de varios
eventos simultáneos. Así, un nodo OR siempre aumenta el número
de posibles cut set construido durante el análisis, mientras que
un nodo AND aumenta el tamaño (número de elementos) de los
mismos. El algoritmo funciona de arriba a abajo de modo recursivo. Cuando
únicamente quedan eventos primarios, el algoritmo se detiene; entonces
los cut set mínimos para el árbol son los conjuntos más
recientes. El esquema principal del algoritmo puede expresarse con las
siguiente reglas:
Finalmente, los cut set generados son los únicos mínimos.
El algoritmo desarrolla sistemáticamente todos los cut set potenciales.
Desde un punto de vista lógico, la idea de este algoritmo puede
explicarse como un desarrollo de una fórmula DNF mínima que
implique el nodo de la cima.
Grafos dirigidos simples
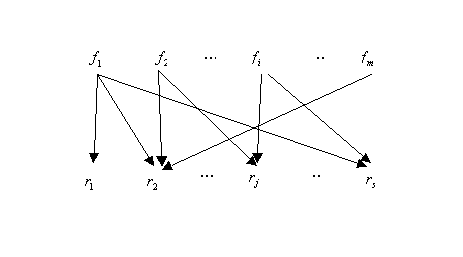
Si fallo =![]() entonces residuo
=
entonces residuo
=![]() ,
,
donde el número de reglas es igual al número de uniones en el grafo. La representación puede ser directa (caso clásico) o difusa, como en [Frank, 1996] y [Frank and Köppen-Seliger, 1995]. Mas adelante se presentan dos formalismos particulares que usan este paradigma.
Para casos prácticos de aplicación, sin embargo, la interpretación
del grafo mediante reglas de inferencia es normalmente ascendente en la
dirección de causalidad. Esto significa que las reglas diagnóstico
toman la forma:
Si residuo =![]() entonces fallo
=
entonces fallo
=![]() es posible
es posible
La ocurrencia de un residuo es la indicación específica de un fallo. Además, pueden interpretarse combinaciones de residuos, y pueden aplicarse reglas de inferencia difusa.
Relaciones de diagnóstico y grafo bipartido de Kö nig
En este caso se utiliza un conjunto finito y discreto de posibles fallos,
Además, se especifica un conjunto finito de manifestaciones,
Los elementos de D y M pueden interpretarse como síntomas o eventos; o desde el punto de vista lógico también como proposiciones lógicas. En el modelo básico se supone que pueden tomar sólo dos valores, 0 si el síntoma no ocurre y 1 si se observa como verdadero.
La relación de diagnóstico es el modelo central usado
para el aislamiento de fallos; es de la forma ![]() .
El significado de
.
El significado de ![]() es
que el fallo elemental
es
que el fallo elemental ![]() es la causa de la manifestación
es la causa de la manifestación ![]() ,
si
,
si ![]() ocurre entonces
ocurre entonces ![]() es
observada.
es
observada.
La relación de diagnóstico ![]() puede representarse en forma de matriz de diagnóstico (binaria)
o en forma de grafo bipartido de Kö nig [Koscielny,
1994] y [Koscielny, 1995];
el grafo también se denota también como
puede representarse en forma de matriz de diagnóstico (binaria)
o en forma de grafo bipartido de Kö nig [Koscielny,
1994] y [Koscielny, 1995];
el grafo también se denota también como ![]() .
Un ejemplo de grafo es el siguiente.
.
Un ejemplo de grafo es el siguiente.
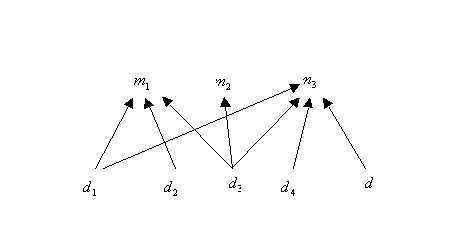
El procedimiento de diagnóstico consiste en el aislamiento de
los fallos. Para los valores conocidos de manifestaciones deben encontrarse
todos los subconjuntos (mínimos) del conjunto de diagnósticos
elementales, tales que asumir que ocurran constituya una explicación
satisfactoria de la configuración de manifestaciones observada.
Así, un diagnóstico es cualquier conjunto mínimo ![]() tal que
tal que ![]() , donde
, donde ![]() es la forma de manifestación observada que debe ser explicada mediante
un diagnóstico. Por ejemplo, si la forma de manifestación
observada se define como
es la forma de manifestación observada que debe ser explicada mediante
un diagnóstico. Por ejemplo, si la forma de manifestación
observada se define como ![]() ,
entonces los diagnósticos mínimos son
,
entonces los diagnósticos mínimos son ![]() ,
, ![]() y
y ![]() . Asumiendo un solo
fallo, el único diagnóstico es
. Asumiendo un solo
fallo, el único diagnóstico es ![]() .
.
El algoritmo diagnóstico constituye una simple pero especifica inferencia abductiva. Puede realizarse de muchas maneras, incluyendo la evaluación sistemática de todos los subconjuntos de D; en este caso sería razonable empezar por subconjuntos de un solo elemento de D y detener el análisis para cualquier subconjunto que cause más manifestaciones que las observadas; por supuesto, para una solución generada que cause exactamente las manifestaciones observadas ningún conjunto superior debe ser analizado.
Un algoritmo más eficaz puede ser el análisis abductivo
del conjunto de manifestaciones observadas. Las siguientes reglas resumen
la idea principal:
Este algoritmo es similar al algoritmo del mínimo cut-set
presentado anteriormente. De hecho, considerando las manifestaciones como
conectadas por puertas AND (todas deben explicarse), y el conjunto de diagnósticos
elementales conectado a una manifestación como entradas de una puerta
OR, la operación más difícil consiste en reducir el
diagnóstico temporal a su forma canónica (de tipo DNF). Una
diferencia visible es que admite sólo un nivel de conexiones (ningún
nodo intermedio) y la eliminación de ciertos diagnósticos
potenciales incoherentes con la observación que ciertas manifestaciones
son falsas.
Modelo Set Covering
Dados estos dos conjuntos y la relación causal, pueden definirse
los siguientes conjuntos:
para cualquier ![]() y
y ![]() . El primer conjunto,
. El primer conjunto, ![]() ,
denota todas las posibles manifestaciones causadas por desordenes específicos,
mientras el segundo,
,
denota todas las posibles manifestaciones causadas por desordenes específicos,
mientras el segundo, ![]() ,
denota todo los desórdenes alternativos que pueden causar manifestaciones
específicas. Finalmente, para un conjunto de manifestaciones observadas
dado
,
denota todo los desórdenes alternativos que pueden causar manifestaciones
específicas. Finalmente, para un conjunto de manifestaciones observadas
dado ![]() tal que
tal que ![]() ,
Un problema de diagnóstico se especifica mediante la cuádrupla
,
Un problema de diagnóstico se especifica mediante la cuádrupla ![]() .
.
Ahora se pueden buscar todas las posibles explicaciones. Obviamente,
es conveniente considerar sólo las mínimas, tales que ningún
subconjunto de ellas sea una explicación del conjunto completo de
manifestaciones observadas. Así, dado un problema de diagnóstico,
una explicación es un conjunto ![]() ,
tal que
,
tal que ![]() ( D´ cubre
o explica totalmente
( D´ cubre
o explica totalmente ![]() ),
y tal que no existe ninguna otra explicación
),
y tal que no existe ninguna otra explicación ![]() que satisfaga la condición anterior (D´ es mínimo con
respecto a la inclusión). La definición presentada es ligeramente
más general que la de [Reggia
et al, 1983]; en el articulo original la solución preferida
es la mínima con respecto al número de elementos.
que satisfaga la condición anterior (D´ es mínimo con
respecto a la inclusión). La definición presentada es ligeramente
más general que la de [Reggia
et al, 1983]; en el articulo original la solución preferida
es la mínima con respecto al número de elementos.
Este tipo de modelo es bastante similar al anterior, basado en relaciones de diagnóstico. La diferencia principal consiste en que admite causalidad débil. Como resultado, puede esperarse un mayor número de diagnósticos potenciales, puesto que los diagnósticos potenciales no se limitan a los que ''encajan exactamente'' con las manifestaciones observadas.
A destacar también que la solución - en el caso general
- no es necesariamente única; varios conjuntos, incomparables con
respecto a la inclusión, pueden formar explicaciones mínimas.
Consideremos el problema de generación de diagnósticos como
un caso específico de inferencia abductiva. Para cualquier manifestación ![]() debe buscarse una lista disyuntiva de posibles causas. Examinando las manifestaciones
sucesivamente observadas se generan varios conjuntos. Cada vez que se genera
un nuevo conjunto, éste debe combinarse con la solución temporal
exactamente como en el modelo anterior. Las soluciones no-mínimas
se eliminan totalmente. Cualquier conjunto final de causas iniciales explica
totalmente las manifestaciones observadas, y es mínimo. Puede, sin
embargo, contener causas primarias que sean causas potenciales de otras
manifestaciones que no se observan en el estado actual del sistema.
debe buscarse una lista disyuntiva de posibles causas. Examinando las manifestaciones
sucesivamente observadas se generan varios conjuntos. Cada vez que se genera
un nuevo conjunto, éste debe combinarse con la solución temporal
exactamente como en el modelo anterior. Las soluciones no-mínimas
se eliminan totalmente. Cualquier conjunto final de causas iniciales explica
totalmente las manifestaciones observadas, y es mínimo. Puede, sin
embargo, contener causas primarias que sean causas potenciales de otras
manifestaciones que no se observan en el estado actual del sistema.
Signed directed graphs - SDG
Un SDG consiste en nodos que representan variables de estado, condiciones de alarma, fuentes de fallos o valores medidos, y ramas (bordes) representando la influencia entre los nodos. La influencia puede ser positiva (' + ') o negativa (' - '). Un nodo puede influir sobre varios de los otros nodos. Cualquier nodo puede ser influenciado por ninguno, uno o varios nodos. También puede especificarse información auxiliar; incluyendo retardos, la intensidad de la influencia, probabilidades, etc.
La representación es muy simple pero muy intuitiva, y para la
supervision y el diagnostico puede resultar satisfactoria en muchos casos.
Sin embargo para asegurar un buen funcionamiento, deben aceptarse varias
limitaciones:
El grafo causal puede usarse tanto para el modelado de fallos (simulación
de propagación fallos) como para el diagnóstico (buscando
causas iniciales de los funcionamientos defectuosos observados). De hecho,
estas dos actividades son aproximadamente duales (o inversas) . Es necesario
asumir fallos en un solo nodo para posibilitar la generación de
árboles dirigidos que muestren la propagación del fallo.
Normalmente pueden generarse varios árboles desde un solo nodo.
Cualquiera de estos árboles constituye una interpretación
de propagación del fallo. Normalmente, solo uno de los árboles
(o una parte de él) muestra los caminos reales de propagación
del fallo, los otros se refieren a posibles interpretaciones que representan
posibles comportamientos potenciales. La propagación de fallos involucra
la construcción de todo este árbol que representa la posible
propagación del fallo. La tarea de diagnóstico consiste en
identificar todos los nodos de raíz provistos de valores cualitativos
(medidos) de las variables del sistema. La opción típica
para estos valores consiste de grande (+1), normal (0) pequeño (-1).
Consideremos un grafo simple presentado en la siguiente figura.
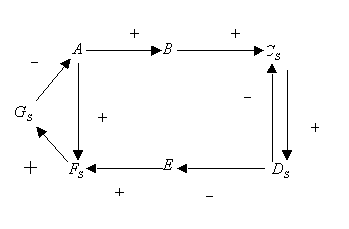
Consideremos que el fallo entra en la red en el nodo A que cambia su
valor de normal (0) a alto (+1). Si consideramos que los nodos B y E no
son medidos, puede simplificarse el grafo inicial mediante node-lumping
a la forma presentada a continuación,; este procedimiento ' elimina
' todas las variables no medidas, asi como las que no tienen ningún
interés (excepto como nodos de raíz potenciales, que no es
el caso). De hecho, estos nodos no proporcionan nueva información
comprobable. Además, se ha eliminado la unión de ![]() a A, puesto que se asume que las perturbaciones positivas son suficientemente
importantes para predominar sobre la realimentación negativa. El
grafo simplificado resultante se presenta a continuación.
a A, puesto que se asume que las perturbaciones positivas son suficientemente
importantes para predominar sobre la realimentación negativa. El
grafo simplificado resultante se presenta a continuación.
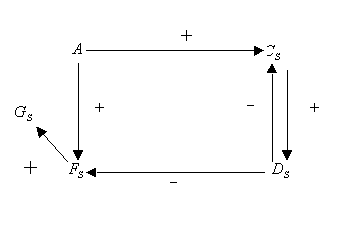
Destaquemos que este grafo todavía contiene una realimentación
negativa. Consideremos ahora los posibles caminos de propagación
del fallo. Primero, puede propagarse de A a ![]() y
después a
y
después a ![]() . Simultáneamente,
puede propagarse de A a
. Simultáneamente,
puede propagarse de A a ![]() y,
a través del lazo cerrado, a
y,
a través del lazo cerrado, a ![]() .
Debido a la asunción de una sola transición de estado, C
no puede volver al valor normal por la realimentación. Semejantemente,
en esta interpretación
.
Debido a la asunción de una sola transición de estado, C
no puede volver al valor normal por la realimentación. Semejantemente,
en esta interpretación ![]() no
pueden cambiarse a pequeño a normal a través de influencia
negativo de
no
pueden cambiarse a pequeño a normal a través de influencia
negativo de ![]() . Esta interpretación
es muestra a continuación.
. Esta interpretación
es muestra a continuación.
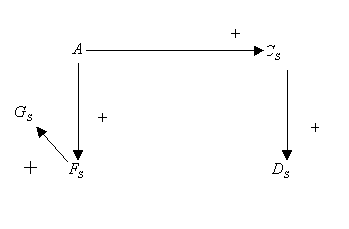
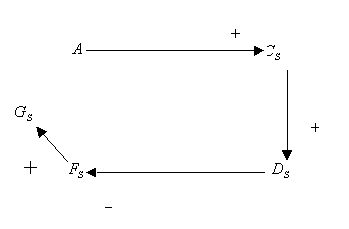
Los árboles de interpretación definen posibles modelos en estado estacionario como ocurrencias de fallos. El fallo, observado como perturbación del valor de la variable, sólo puede propagarse en el árbol hacia abajo, desde nodo de la raíz, según los signos de las uniones. Puede detenerse en algunas variables antes de alcanzar las hojas, sin embargo, debido a la asunción que no puede haber un hueco en el camino de propagación del fallo, si cierta variable en un camino seleccionado es perturbada, entonces todas las variables anteriores también deben ser igualmente influenciadas. Para las dos interpretaciones presentadas, los modelos de propagación de fallo son los de las tablas.