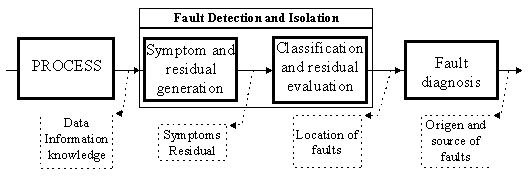
Fig. .2 Schematic representation of the procedure of fault diagnosis.
1.4 Fault detection: structures and methodologiesNowadays, the interest for supervision is increasing due to the growing demands for quality, safety, reliability, availability and cost efficiency in industrial processes. As systems grow in size and complexity, the possibility of misbehaviour increases. Thus, the call for fault tolerant systems is gaining more and more importance. Fault tolerance could be achieved either by passive or active techniques [Frank and Köppen-Seliger, 1995] :
In this work, only active approach is taken into account. This chapter
overviews different methodologies that can be applied in this sense to
remark the importance of human knowledge about process behaviour and how
it can be used to implement supervisory structures. Finally, it is concluded
that the use of both, analytical and knowledge-based methods, together
can improve the results of supervisory structures. In such cases, the main
problem is about integration of methods provoked by differences in data
representation (numeric, qualitative, symbolic).
Fault detection: structures and methodologies.
Supervision is essentially the set of techniques used with the goal of assuring the integrity of a system. The definition given in the last paragraph assigns to supervision the role of detecting (to recognise and to indicate) in real time abnormal behaviour of a process taken benefit of all information available about the process (measures, models, history, experience and so on).
According to these goals, the main part of supervision of a complex system is focused on to detect and isolate occurring faults and provide information about their size and source, [Frank and Köppen-Seliger, 1995]. The most important and difficult task is centred on fault detection and diagnosis where difficulty increases with the real time constraints and complexity of systems (non-linear, coupled dynamics, time dependencies, etc.). The core of the fault diagnosis methodology is the so-called model-based approach, where either analytical or knowledge-based models or combination of both are used in combination with analytical or heuristic reasoning [Frank and Köppen-Seliger, 1995]. The classical procedure of a fault diagnosis system is depicted in Fig. 2.2. This is achieved in three basic steps, residual generation, evaluation and analysis, not always clearly separable.

Fig. .2 Schematic representation of the procedure of fault diagnosis.
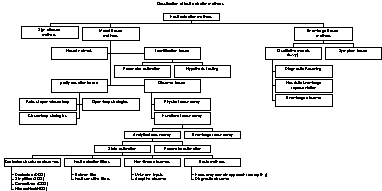
Fig. .3 Classification of fault detection methods [Pal, 1995].
In the following subsections, fault detection methods are briefly described and classified in model, signal and knowledge-based methods. Model-based methods group analytical methods based on comparing process output with theoretical model response to the same input applied real process. The next subsection, signal based methods, is restricted to those methods that only use process output variables in the fault detection task and no model is used. Finally, the knowledge-based method subsection, introduces the problematic of dealing with knowledge representation to monitor and supervise dynamic systems.
Model-based fault detection.
Model-based fault detection methods are focused on residual generation, i.e. fault indicators (Fig. 2.4). Residuals are obtained as changes or discrepancies in special features of the process obtained from process variables (for example, output signals, state variables) or coefficients (for example, estimated parameters or other calculated ratios). To achieve this goal, data obtained from the process is compared to the data supplied by models representing normal operating conditions. For this, different change detection methods are applied. The next step consist in residual evaluation to decide about faults existence. Threshold logic, statistical decision theory, pattern recognition, fuzzy decision making or neural networks are actual methods used to decide whether and where a fault has occurred.
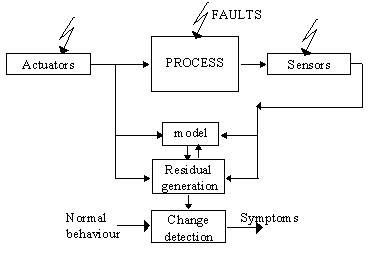
Fig. .4 Architecture of a model-based diagnostic system from [Maquin and Ragot, 1996].
Different kinds of process models and methods can be used to generate residuals of state or output variables. A basic classification of them is represented in Fig. 2.5. Observer-based residual generation consists in using observers or Kalman filters to reconstruct the interest output of the system. Then, the error between real data and estimated data or a function of them are used as residual. In the parity space approach the process equations (for instance, state space equations) are modified with the aim of getting residuals decoupled from system states and different faults. The inconsistency of these parity equations represent the residuals. On the other hand parameter estimation methods are based on the assumption that the faults are provoked by changes in the physical system parameters (mass, friction, resistance, viscosity, etc.). Therefore, these methods use process measures to repeatedly estimate the parameters of the actual process. Estimations are compared with the parameters of the reference model, obtained under fault-free conditions. A wider description of those methods and other interesting variants of them are included in [Frank, 1996].
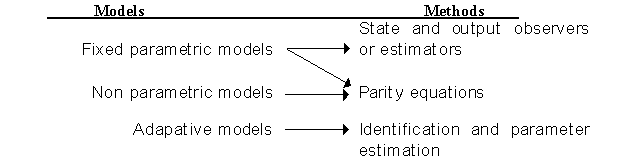
Fig. .5 Dependency between method and model to be used in a model-based fault detection.
Although these approaches have proved to be very effective in many applications, they have two major shortcomings : the complex technology or natural process are generally non-linear time-varying systems, which makes it particularly difficult to detect structural changes in the system and to obtain adequate models for this purpose. Secondly, the available model is often assumed to represent normal operating conditions, and the impact of a departure from these conditions on the model outputs is difficult to predict [Du, Elbastawi and Wu, 1995a]. Consequently, these methods are difficult to be applied to dynamic process submitted to repeated changes in the operation mode.
Model-based fault detection requires process variables (measures) to compare real process response and model response. This comparison is performed under the assumption that the same input is provided to both systems. Therefore, process measures and actions must also be supplied as input of model. Other methods can be applied if only process output is available, i.e. signal-based methods. This methods are usually used with rotating machinery and electrical circuits and applied with signals measured from process in steady state. Therefore, signals are thought to be rich in information. This is the case of vibrations analysis and other methods based on frequency analysis.
Signal-based methods are focused on analysing signal features. Change detection is measured as a deviation from normal behaviour. For this purpose, statistical (mean, variance, entropy, etc. are estimated), freqüencial (as filtering or spectral estimations methods for example) and probabilistic (Bayes decision) methods are used. Signal models or patterns are used to detect deviations from normal operating modes. Those methods do not require the mathematical model of process. Knowledge about system is assumed to consist in learning associations between process measures and operating conditions. In this sense they can be considered as knowledge-based methods.
Some of the limitations of pattern recognition techniques is that they assume a knowledge about all systems states and do not take into account the time evolution of the process under study. A survey of these techniques can be consulted in [Denoeux, Masson and Debuisson, 1996].
In the case of noticeable modelling uncertainty, a more suitable strategy is that of using knowledge-based techniques. Instead of output signals any kind of symptoms can be used and the robustness can be attained by restricting to only those symptoms that are not strongly dependent upon the systems uncertainty. In this case, knowledge has to be processed which is commonly incomplete and can not be represented by analytical models. On the other hand, residual evaluation is a complex logical process which demands intelligent decision making techniques, like fault tracing in fault trees or Petri nets or pattern recognition including fuzzy or neural techniques. Therefore, knowledge-based methods are quite a natural approach also for residual generation in fault diagnosis, and ESs have so far been applied more successfully here than in the field of control ([Frank, 1996]). The use of knowledge, in the model definition or qualitative observation of variables, when analytical models are difficult to be obtained, is another field where AI techniques can be used.
Knowledge-based methods is a field in continuous evolution, where AI techniques have an important role. There is not a unified theory to be applied to these methods and, in fact, knowledge-based methods can be applied in all three phases of fault diagnosis, namely residual generation, residual evaluation and fault analysis, although the phases in this case are not always as clearly separable as in case of the analytical approach. [Frank, 1996] distinguishes two categories in the knowledge-based domain for diagnosis, also applied for residual generation:
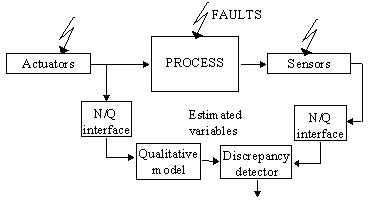
The use of one or the other method is only submitted to the knowledge about process behaviour or faults. Furthermore, there are not exclusive methodologies and a combination of both can be required. In fact, the best strategy tries to use all available knowledge and data for reaching the fault detection goal.Additional problems, when dealing with knowledge representation, of process behaviour or faults description, occur when interfacing fault detection structure (linguistic representation of magnitudes and process variables) and process (numerical variables, measures). However, the use of all available information, i.e. numerical data and knowledge, can improve fault detection structures because they are complementary approaches.
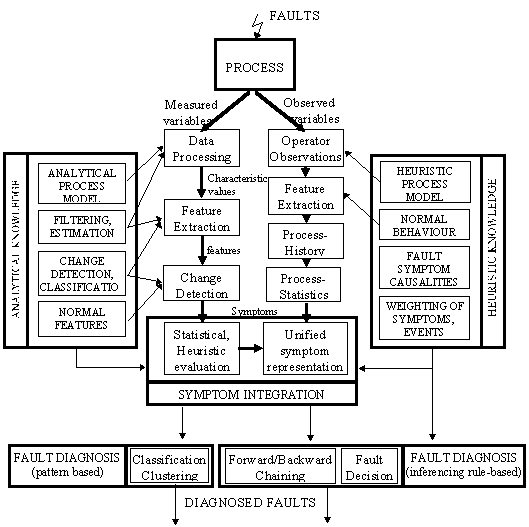
Fig. .7 Scheme of knowledge-based
fault detection based on
symptom generation (From [Isermann
and Ballé, 1996])
Fig. 2.7 represents how both, numerical techniques and knowledge-based techniques, can be merged for fault detection. In fact, heuristic knowledge acquired from process observations is used in this proposal to reinforce analytical methods applied to numerical variables in the symptoms generation step. While numerical methods are used for features extraction of measured variables, i.e. signal processing techniques as filtering and analytical estimations, some drawbacks appear in extracting features from operator observations. Specialised knowledge processing techniques must be used with this aim. Taking into account that difficulties in such systems are presented at knowledge representation level, the use of those techniques for features extracting are not very extended.