This section is devoted to presentation of a diagnostic example of simple single-tank system.
Diagnostic Problem
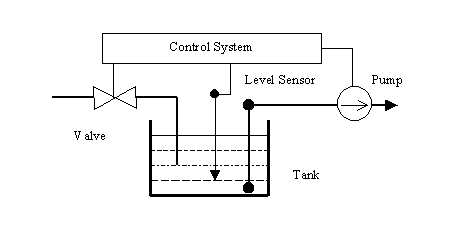
In this section a simple example of a diagnostic problem and its solutions are presented. The diagnostic problem concerns a small system (possibly a part of a bigger one) composed of a tank, water supply system controlled with valve, water removing system driven by pump and level sensor . The system is shown schematically on the figure below.

The basic analysis of the system behaviour is as follows. The tank should normally contain certain amount of water provided through the valve. If the level is too low the valve can be opened and water flows into the tank. Its level is controlled with a single level sensor providing the possibility to close the valve after the required level is achieved. The pump is normally used to remove the water after finishing the operation of the system. If by some accident the level is too high, the pump removing the water is also started. It is assumed that both the valve and the pump are controlled (according to some control algorithm) with use of signals from level sensor and from the control system. For the sake of security the system is made safe by double protection system; whenever the level of water is too high,not only the valve should be closed, but the pump should be switched on, as well. Further, we assume that the capacity of the pump is greater than the one of the water supplying valve. This implies that even if the valve is opened, it is normally enough to set on the pump to protect an overflow.
One can consider two kinds of expected behaviour of the system with respect to the water level. The normal expected behaviour of the system is to keep the level of the water within some predefined limits. The abnormal expected behaviour may consist in an overflow, i.e. a
situation when the level is too high. Let us consider the latter case, i.e. we are interested with defining, detecting and diagnosing the explicit fault rather than any abnormality occurring. The fault of interest is just one, i.e. water overflow. Let us describe different stages of diagnostic procedure following from the proposed approach.
For illustration, let us assume that the partial state
representation is a logic-like formula of the form ![]() for normal operation, where the meaning of
for normal operation, where the meaning of ![]() is
that the level of the water is higher than some level denoted with low
and lower than the one denoted with high.
is
that the level of the water is higher than some level denoted with low
and lower than the one denoted with high.
Now let us consider a formula describing all the states
(a situation in our terminology, i.e. a set of states) in which overflow
occurs. The formula may be of the form ![]() .
The failure detection problem consists in checking if the current state
belongs to the failure situation. This can be done by formulae matching
with respect to their generality; a more general formula describes a bigger
set of states. Assume that the level denoted symbolically as very_high
is higher than the one of max (in practical system these may be
just ordinary numbers). Let the current state formula be
.
The failure detection problem consists in checking if the current state
belongs to the failure situation. This can be done by formulae matching
with respect to their generality; a more general formula describes a bigger
set of states. Assume that the level denoted symbolically as very_high
is higher than the one of max (in practical system these may be
just ordinary numbers). Let the current state formula be ![]() ,
where
,
where ![]() denotes the rest
of the fats true in the particular state. Thus in our case
denotes the rest
of the fats true in the particular state. Thus in our case
![]()
In fact, in any state described with the right hand formula
above , the failure characteristics specified by the formula ![]() must hold; the crucial element of the check consists in verifying that
must hold; the crucial element of the check consists in verifying that ![]() .
.
The list of symptoms considered with respect to the example is as follows; they are structured into elementary diagnoses, intermediate symptoms and failure manifestations.
Manifestations, here single failure symptom:
m -- water pouring out of the tank,
Intermediate symptoms:
v1 - valve_open,
v2 - pump_off,
v3 - valve_stuck_in_open_position,
v4 - valve_open_by_control_signal,
v5 - pump_off_by_power_off,
v6 - pump_off_by_control,
v7 - pump_blocked,
v8 - pump_on_by_control,
v9 - valve_open_signal_operating,
v10 - pump_on_signal_from_level_sensor_operating,
v11 - pump_on_signal_from_control_system_operating,
v12 - power_off,
v13 - valve_open_signal_from_level_sensor_on,
Input symptoms - elementary diagnoses:
d1 - valve_stuck_in_open_position_fault,
d2 -valve_open_control_signal_on,
d3 - level_sensor_on_when_level_too_high,
d4 - pump_on_by_control,
d5 - pump_broken_fault,
d6 - power_on.
As one can see, the intermediate symptoms include ones observable (e.g. v2, v5) and non-observable (e.g. v3). Some of the symptoms may be ``artificially'' introduced to assure clear presentation of the graph and protecting distinction between node types (e.g. v10, v11) (avoid type mixing). The initial symptoms cover both elementary diagnoses referring to element faults (e.g. d1, d3), as well as faulty control signals (e.g. d2, d4) and external conditions (e.g. d6).
The causal graph is constructed by analysis of causal dependencies among symptoms and encoding them with node structures. The selection of AND, OR, and NOT nodes helps to express most common phenomena referring to logical functions. NOT nodes are also used to represent symptoms negations. The structure of the causal graph is presented on the figure below.
[here: grapf1.eps
On the picture symptoms (nodes) found to be true are marked with filled circles; the empty circles denote false symptoms or ones of unknown status. After identification of the failure, only the node marked with m is found to be true. When further observations are accessible, also v2 and d6 are marked true.
In order to present the elements of diagnostic reasoning
let us consider a particular diagnostic problem, e.g. one given by ![]() and
and ![]() , i.e. the overflow
of water when the system is switched on and the pump is observed not to
work. The problem is to find diagnoses explaining m and consistent with
the observations.
, i.e. the overflow
of water when the system is switched on and the pump is observed not to
work. The problem is to find diagnoses explaining m and consistent with
the observations.
Before we start the analysis, let us propagate the observations through the graph. In fact, only d6=true can be propagated. We obtain v12=false and v5=false; this information can be used for checking consistency with hypothesized diagnoses.
Let us start the analysis from the failure manifestation. In fact, we perform backward, top-down search. As the symptom meaning a failure m is identified, we search for the possible reasons for that; the search is performed backwards, i.e. we look for possible explanations. With respect to our model there is one conjunctive cause possible, i.e. v1=true AND v2=true. The procedure must recursively explain both the symptoms found. Note that v2=true is consistent with the observations (in other case there would be an inconsistency).
Now for explaining v1=true one can suggest two hypotheses, namely v3=true or v4=true. We follow the latter one leaving the first one for further possible exploration (in the algorithm it is saved on the stack). For explanation of v4=true again we have two possibilities; let assume that we select v13 to be true and thus we must have d3=false as the consequent selection; the process of explaining v1 is stopped here since we have arrived at an initial node being an elementary diagnosis. All the other possibilities of explaining v1=true are left for further possible use, while now the problem is to explain v2=true.
For v2=true there are three possibilities. Note that,
however, the first one, i.e. v5=true is inconsistent with observations,
so it should be left unexplored. Assume we select the second one, i.e.
v6=true. Further on, the only explanation of v6/true is v8=false,
which is consistent with the observations. And to explain v8=false
we must assume that both v10=false and v11=false hold. This
implies d3=false (already found on another way), and d4=false.
The final diagnosis is then given by ![]() ,
i.e. the level sensor is faulty and no control signal for setting on the
pump is provided while the system is on. The further analysis of the diagnosis
may lead to detection of one hard fault (element fault, d3=false),
finding one control signal set to 0 (if this is a fault it should follow
from a further analysis of the control algorithm for the specific conditions),
and one operational condition already observed. Of course, this is only
a potential diagnosis, and as such it should be verified, e.g. by checking
the level sensor and measuring the control signal value. Moreover, several
other diagnoses can be found by exploring the other alternative explanations
of symptoms, temporarily left pending for further use.
,
i.e. the level sensor is faulty and no control signal for setting on the
pump is provided while the system is on. The further analysis of the diagnosis
may lead to detection of one hard fault (element fault, d3=false),
finding one control signal set to 0 (if this is a fault it should follow
from a further analysis of the control algorithm for the specific conditions),
and one operational condition already observed. Of course, this is only
a potential diagnosis, and as such it should be verified, e.g. by checking
the level sensor and measuring the control signal value. Moreover, several
other diagnoses can be found by exploring the other alternative explanations
of symptoms, temporarily left pending for further use.
The set of all possible diagnoses consistent with the
observations found by the algorithm is:
and only four of them are minimal diagnoses (i.e.
2,3,4 and 6) in the sense of set inclusion. But with respect to the subgraph
generated , all the six diagnoses consist different solutions. For information,
for the above problem specified with no initial observations there are
as many as 14 potential solutions, and 6 of them are minimal with respect
to set inclusion.
The final result is a diagnosis, i.e. a set of elementary diagnoses, usually a minimal one, such that assuming that the listed components are faulty, an explanation of the observed failure is generated with respect to the causal graph. Note that obtaining a diagnosis is performed by finding a solution subgraph constituting an explanation of the observed failure. Such a subgraph for the examined system is shown with thicker lines in the figure below. The symptoms found true are marked with filled circles.
[Here. grapf2.eps
A more complex, three tank examples diagnostic problems
can be found in.....