7.5 Rule-based systems, decision tables, and decision trees in state monitoring and situation classification control and decision support   Rule-based systems, decision tables, and decision trees: common characteristics
Application of rule-based systems, decision tables, and decision trees in state monitoring, situation classification (situation assessment) and decision support is similar from both technical point of view and intended aims. All of the mentioned tools are working according to similar principles and differ mainly with respect to internal knowledge representation scheme and details concerning inference control mechanism. Hence, in many application the selection of particular tool is arbitrary, and may depend on individual preferences, size of the problem to be solved, type of underlying logic (propositional vs. predicate logic), etc. However, the main basic scheme of operation remain the same: for a given input state description, find the appropriate pattern matching it (rule precondition, condition part of decision table or sequence of conditions in a decision tree), and finally select the appropriate item (rule of rule-based system, row or column of a decision table, decision path in decision tree) and execute it. The basic mode of work is illustrated with the figure below.
 
 



 


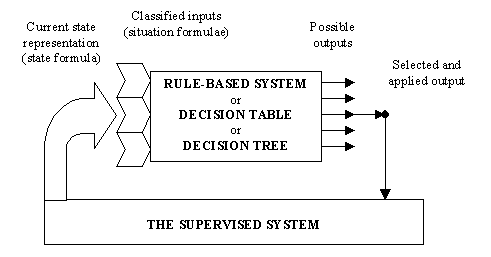
Thus the basic scheme of operation is the same for all of the discussed tools. Below some particular problem concerning implementation and application will be presented. We start with situation recognition or situation assessment which is also the basic mechanism checking if and which rule preconditions, decision table conditional part or decision tree sequence recognition.

Situation recognition   Detection of specific situations, verification of rule precondition satisfaction, detection of faults, detection of occurrence of specific behaviour patterns, etc. using any of the presented languages for knowledge representation consists basically in application of the same mechanism: this is pattern matching. The principal idea consists in matching the current state description against the specific situation formula and checking if generalisation holds. Further, if necessary, specific values of parameters are determined.

It is possible to use a combination of knowledge representation formalisms - in such a case the formulae representing the total information should be composed of separate parts expressed with use of a single formalism. For simplicity of the discussion we assume that one of the formalism has been chosen. The extension to simultaneous use of several formalism (knowledge representation language) is straightforward.

The basic assumption is that the state of the system is monitored, and with respect to the application of an appropriate signal-to-symbol transformation approach a formula describing current state is formed at certain time intervals. Such a formula -- to be denoted with  - keeps the information about current state, i.e. systems parameters, relations holding, etc. for an assumed duration of time, sometimes referred to as time window. Note that in fact it is not necessary to write the formula explicitly - certain components should be just accessible if necessary.

Now let us suppose that for identification of specific situations or (preconditions, failures, etc.) of the considered system a set of formulae defining (and simultaneously describing) certain expected ones was defined. Let 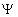 be a set of situation formulae defining possible situations of interest and let 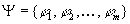, where each 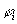 is a situation formula defining certain type of situation.

The problem of identifying specific situation defined with formula 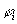 can be now replaced by checking if this formula generalises a formula  describing current state, i.e. if
 
 

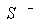As the methods for verification of generalisation among formulae have been presented, the only remaining problem is to systematically evaluate all the situation formulae 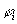 with respect to current state description. In case for some  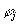generalisation holds, the specific situation defined with  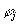is confirmed to occur. Further, there can be simultaneous occurrence of several specific situations (e.g. preconditions of several rules may be satisfied simultaneously or multiple failures occur) at a time. Problems of practical implementation: a general outline   A number of practical applications are reported in literature (see some of the enclosed references). In [Laffey et al, 1988] the problems concerning real-time applications of knowledge-based systems are discussed. These problems apply to control support, monitoring and supervision and decision support knowledge-based systems. Among other, the following features distinguish real-time implementations:
 
  • Nonmonotonicity: Incoming sensor data and facts which are asserted to the system knowledge-base do not remain static during the entire run of the program.
  • Continuous operation: A real-time system must be capable of continuous operation, even after partial or complete failure of one or more components of the controlled system.
  • Asynchronous events: A real-time system must be capable of being interrupted while in normal operation, so as to accept input data from an unscheduled or asynchronous event and react in an appropriate way.
  • Interface to external environment: A real-time expert system typically needs to be coupled to input sensors and actuators.
  • Uncertain or missing data: A real-time system must be able to recognise and appropriately process data of uncertain or diminished validity.
  • High performance: A very high capability of fast information processing (high performance) constitutes a typical requirement for knowledge-based real-time systems; this is due to short response time and complex nature of both data and data processing methods.
  • Temporal reasoning: A real-time systems typically needs the ability to reason about past, present and future events, as well as the sequence in which the events happen.
  • Focus attention: When a significant event occurs, it is important that the real-time system be able to focus its resources on important goals.
  • Guaranteed response time: The system must be able to respond by the time the response is needed. Moreover, usually the best possible response within the given deadline is required.
  • Integration with procedural components: A real-time knowledge-based system must typically be integrated with a conventional real-time software for accomplishing tasks such as signal processing, feature extraction and application of specific input/output algorithms.
    •


    Note that most of the above features are in one or another way represented and dealt with in any knowledge-based control and supervision systems. The paper [Laffey et al, 1988] outlines about fifty different applications ranging from aeronautical and space systems to communication, financial, medical, and automatic control applications, including robotic and autonomous vehicle implementations. One of a most appealing examples consists of a real-time expert system controlling a robot ping-pong player.

    A number of applications in more classical domains of automatic control are reported as well. In some review papers applications of knowledge-based systems to expert supervisory control, supervision, diagnosis, and control in the domain of automatics are reported [Tzafestas, 1987], [Tzafestas, 1989], [Tzafestas 1989a]. Example applications include self-tuning PID controller, a rule-based self-tuning supervisor, an expert system for distillation control synthesis, and expert supervisory control of a turbo-charged diesel engine.

     Selected technical problems   In this section we shall discuss some of the problems concerning implementation of knowledge-based systems, using mainly rule-based methodology. Depending on the specific application and the desired characteristics of a supervision knowledge-based system, a number of practical problems which are usually not considered within the theoretical framework occur. The problems are of heterogeneous nature. However, with regard to the general structure of a knowledge-based monitoring and supervision systems one can try to distinguish the four following basic groups of them:
     
  • Input problems - these are problems concerning the input of signals coming from the environment and the system to be controlled as well as further `transformation' of the signals into the accepted knowledge representation form, i.e. logical formulae,
  • Output problems - these problems concern the output of the knowledge-based control system, in particular `transformation' of the appropriate part of the knowledge represented in logical form into control actions and further execution of the required operations,
  • Knowledge representation problems - i.e. problems of internal knowledge representation; these problems are in fact three-fold: first, what part of knowledge should be in fact represented explicitly and what knowledge can be dealt with in an implicit way, second, how to encode and organise the knowledge base, and third, how should the knowledge be managed and updated,
  • Reasoning problems - these are the problems concerning reasoning strategy and other details, and they include rule selection or conflict resolution mechanism, efficient matching algorithms, dealing with specific predicates, functions and constants, and reasoning with use of implicitly represented knowledge, etc.
    •


    For the above problems one cannot provide a general theory and practical solutions depend on the specific problem. Moreover, the presented above classification referring to the structure of supervision systems is to a high degree a matter of convention. In fact, all the problems are strongly interconnected and selection of a solution to certain problems in one of the above-indicated groups can project on and significantly influence the solutions of other problems in different groups. Among the areas of mutual penetration one can distinguish at least two of great importance. First, the input and output problems interleave with the knowledge representation ones, and second, the knowledge representation problems influence the solutions of reasoning problems.
    The input and output problems are to certain degree similar, since both of them concern the problems of interface between knowledge-based supervision system and environment. Practical solutions depend on the character of signals (electrical, mechanical, chemical, biological, etc.), acquisition possibility (detection, measurement, observation, etc.), possibility of performing control actions, accessible sensors and actuators, required accuracy, etc. Practical solutions may include the application of abundant variety of instruments used in classical and non-classical automatic control, including cameras and image processing and interpretation systems for input, as well as robotic or manipulator systems capable of performing complex mechanical operations for output.
    Knowledge representation problems are strongly interconnected with reasoning problems. The basic problem of knowledge representation concerns the practical representation of state formulae. The theoretical introduction and presentation in Chapter 4 and 6 provides only a general framework which should be adjusted to any specific case.
    Types of facts and their representation   One can notice that it is not necessary (and maybe unreasonable) to keep all the knowledge concerning current state in the computer memory in form of facts. Note that, in general, among all the facts at least the following types can be distinguished with regard to implementation problems:
     
  • ordinary facts, representing relations holding in the supervised system, but not accessed via input channels,
  • facts representing the internal state of the knowledge-based supervisory system memory, such as control goal, status, certain semaphores, history, etc.,
  • input facts, which can be always generated with respect to recent input parameter values,
  • user input facts, i.e. facts which can be obtained from the user-supervisor only (if one exists),
  • deducible facts, i.e. facts which represent somewhat redundant information and can be easily deduced with use of other existing facts,
  • facts representing mathematical (arithmetical) relations, such as greater than or equal to (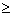), equal (=), etc.,
  • facts representing domain-specific properties which can be evaluated with regard to expert domain knowledge.
    •


    Note that with regard to the above mentioned rough classification of facts only the ones belonging to the first two groups should be necessarily explicitly represented in the knowledge base. It may be unreasonable to keep the input facts and input user facts in the memory, since any time they are necessary they can be `read' from the input interface and the user can be simply asked for them. Finally, deducible, mathematical, and domain-specific facts can be generated according to current needs with use of special inference mechanisms, and probably this would be more efficient than keeping them all the time in the knowledge-base. Using such a partially implicit knowledge representation scheme can significantly contribute to saving the memory required for state representation. Simultaneously, it can speed up execution, since generation of certain facts can be faster than search for them in a large knowledge base and the time required for knowledge base actualisation is significantly reduced. However, implicit knowledge provides additional problems for reasoning mechanism, and particularly for the matching procedures. In case some facts are represented implicitly, direct matching of facts included in some simple formula (possibly the one describing preconditions of some transformation rule) against state formula is no longer satisfactory -- specialised matching procedures covering the generation of implicit facts are required. In general, a trade-off between explicit and implicit knowledge representation must be considered and various factors should be taken into account.

    For practical considerations the following types of facts have been selected:
     

  • state - specified by the basic part of the ,state formula and stored in computer memory,
  • control - special facts specifying state of the controller memory,
  • user - specified by the user, to be read when necessary,
  • input - to be read as input data, to be read when necessary,
  • infer - facts to be inferred according to given rules with use of special inference mechanism,
  • special - interpreted according to special rules, e.g. arithmetical ones.
    •


    As an example it is shown how the above facts are encoded as terms of some meta-facts being Prolog clauses. Any such fact can have a number of arguments apart from the term encoding the logical formula; for the example implementation we have chosen three arguments: type of the logical fact (as above), atom, i.e. the appropriate logical formula, and its current truth-value. The following extract from Prolog program shows the appropriate structure.

    { *** Types of facts *** }

    {

    state - specified by the state formula

    control - special facts specifying state of the controller

    memory

    user - specified by the user

    input - to be read as input data

    infer - fact to be inferred according to given rules

    special - interpreted according to special rules

    The form of any fact in database is:

    fact(<type>,<atom>,<truth-value>).

    and f(<type>,<atom>) for preconditions,

    where:

    <type> = one of the above types,

    <atom> = specification of the atomic formula defining the

    fact,

    <truth_value> = current status; true/false.

    }

    To summarise, one cannot expect a single, universal solution providing a consistent approach to solving practical implementation problems. Further, only the most obvious ones were roughly sketched out in this section. In the following subsections an attempt at analysis of certain particular problems and putting forward some practical guidelines was undertaken. Some of the considerations are supported with simple examples of practical applications.

     Reasoning control mechanism and use of domain heuristics   Another group of problems inevitably connected with any practical implementation of rule-based control systems are the ones concerning the control of reasoning, i.e. the strategy of search for the rules to be applied. Roughly speaking, the basic problem of reasoning control consists in repeated execution of the following cycle:
     


    The above scheme outlines the basic algorithm of reasoning in a knowledge-based control system. The main modifications incorporated in practical applications may concern the following problems:
     

  • Segmentation of the initial set of rules with regard to certain contexts; depending on the current context only the appropriate segment of rules is taken into consideration during the search for a conflict set,
  • Application of various domain-dependent, heuristic conflict resolution mechanisms,
  • Application of specialised matching algorithms and heuristic procedures for pre-selection of rules,
  • Application of specialised computational procedures for determining specific features of the current knowledge-base, e.g. finding some extremal (minimal, maximal) element, calculating the exact number of elements satisfying some conditions, etc.
    •


    Segmentation of rule-base is a commonly used paradigm in a number of different knowledge based systems. The main goal of such segmentation is to reduce the number of rules considered at a time by temporal putting aside the rules which are not applicable. The key to select the rules is the current context. In control systems the context may be defined with regard to the mode of operation, such as for example automatic, semi_automatic, manual_control, etc. Another factor used for determining the context can take into account the current status of operation, for example normal_operation, start, stop, emergency, failure, diagnosis, etc. Note that within a context it is possible to distinguish several subcontexts, and thus perform further segmentation. In this way a natural hierarchy in the set of rules is introduced. The reasoning control mechanism works then in a hierarchical way as well -- it is first to determine the appropriate context (and possibly - subcontext), and next - perform

    standard search and activation cycle taking into account only the limited to the determined context set of rules. Such an approach provides the possibility to speed up execution, but is also important for making the rule-base much more transparent to the user, and thus easier to understand, supervise, modify and debug.

    Conflict resolution mechanisms are usually based on some arbitrary assumptions (such as that the order of rules indicates simultaneously the hierarchy of execution; such an approach constitutes one of the principles of Prolog programming language), or some heuristic rules, for example assigning some numerical priorities to rules. In general, the most typical conflict resolution mechanisms operate with respect to the following possible principles:
     

  • ordered execution of the rules from the knowledge base (only those of them which have the conditional part satisfied); typically a linear order of execution is followed; this include the case of the additional information placed in the next part of the rules -- the specified rules are examined first, and the first selected is applied; this is aimed at speeding up the execution of some typical routines,
  • priority evaluation mechanisms can be applied so as to establish the order of rules in the conflict set; the priority evaluation can take into account different factors such as the number of successful applications of a rule, the time of last application of a rule, the possible values of parameters for the current application of a rule, certain external conditions, etc.; some most simple possibilities include use of most recently applied rule, use of the least recently applied rule, use of the most specific rule, use of the rule with least number of variables, etc.,
  • meta-control knowledge-based system for selection of the rule to be applied can be used; such systems can use typical expert systems approach, and take into account the current goal of reasoning, certain environmental conditions, some statistics concerning the past system behaviour, etc.,
  • context determining facts can be used as semaphores for blocking and enabling the inference control mechanism to limit the subset of rules which can be executed next; in this way dynamic segmentation of the set of all rules can be handled,
  • parameter values approach can also be applied to select the rule with the parameters best satisfying some pre-specified conditions; this method can be regarded as some modification of priority evaluation methods,
  • optimal control approach can be applied by selection of a rule assuring the best value of some performance indicator; in case of planning systems a dynamic programming or heuristic search approach can be applied in order to generate a sequence of rules constituting the optimal solution.
    •


    Of course, a realistic system can combine the above approaches and still use some other ones. However, no general solution can be suggested since the design and implementation of reasoning control is a highly specialised, domain-specific task.

    As an illustration, the basic implemented strategy is a linear search of rules with execution of he first rule found; after execution of the rule the search cycle is repeated. The order of rules specification is equivalent to establishing priorities - the first rule has the highest priority, the second one lower, etc. A simplest implementation can be as follows:

    run:-

    repeat,

    findrule(_Number),

    executerule(_Number),

    test,!.

    findrule(_Number):-

    rule(_Number,_,_Preconditions,_,_,_),

    consistent(_Preconditions),!.

    executerule(_Number):-

    rule(_Number,_,_Preconditions,_,_Dels,_Adds),

    consistent(_Preconditions),

    remove(_Dels),

    add(_Adds).

    test:-

    rule(1,_,_Preconditions,_,_,_),

    consistent(_Preconditions).

    remove([]):- !.

    remove([_F|_T]):- retract(fact(_F)),remove(_T).

    add([]):- !.

    add([_F|_T]):- assert(fact(_F)),add(_T).

    The simplest version of a rule interpreter as presented above uses simplified rule format and the simplest test for rule preconditions. Another version of a rule interpreter for linear search an execution of first rule found is listed below.

    run:-

    write('LOOP'),nl,

    findrule(_Number,_Name,_Preconditions,_Negative_preconditions),

    executerule(_Number,_Name,_Preconditions,_Negative_preconditions),

    !,

    run.

    run:-

    nl,nl,nl, write('No rule applicable; operation halted').

    findrule(_Number,_Name,_Preconditions,_Negative_preconditions):-

    rule(_Number,_Name,_,_Preconditions,_Negative_preconditions,_,_,_,_,_),

    write('Find rule: testing preconditions: '), write(_Number),nl,

    satisfied(_Preconditions),

    unsatisfied(_Negative_preconditions).

    executerule(_Number,_Name,_Preconditions,_Negative_preconditions):-

    rule(_Number,_Name,_,_Preconditions,_Negative_preconditions,

    _Action,_Delete_results,_Add_results,_Message,_Next_rules),

    write('Exec rule: No testing of preconditions: '), write(_Number),nl,

    {satisfied(_Preconditions),

    unsatisfied(_Negative_preconditions), }

    write('Action executed: '),write(_Action),nl,

    remove(_Delete_results),

    add(_Add_results),

    write(' *** INFO *** '),nl,write(_Message),nl.

    remove([]):- !.

    remove([f(_Type,_Term)|_T]):-

    retract(fact(_Type,_Term,_)),remove(_T).

    add([]):- !.

    add([f(_Type,_Term)|_T]):-

    write(_Type),write(' '), write(_Term),nl,

    process(f(_Type,_Term),f(_Type,_New_term)),

    write(f(_Type,_New_term)),nl,

    assert(fact(_Type,_New_term,true)),add(_T).

    process(f(state,angle(plus(_Angle,_Alpha))),f(state,angle(_New_angle))):-

    data(_Alpha,_Given),

    write(_Given),nl,

    _New_angle is _Angle + _Given,

    write(_New_angle),nl,!.

    process(_Term,_Term).

    This version does not test the preconditions of a rule found twice and incorporates different scheme of loop in Prolog.

    In the work [Ligeza, 1993] a modification of the basic interpretation algorithm allowing for flexible switching among rules has been proposed. The idea is that if domain expert knowledge about plausible dynamic reordering of rules is available, it can be encoded with use of the next part of rules. The meaning of this specification is as follows: if, after execution of some rule it is likely/reasonable to try execution of a given sequence of

    rules, the basic linear search can be temporarily abandoned and the specified rules can be tried first. This mechanism allows for very flexible and general reordering of rule execution. In fact, a dynamic LIFO (last in first out) queue is incorporated in the reasoning control mechanism. A ''two-level'' interpreter performing the search and execution according to this strategy can be as follows:

    run:-

    write('LOOP NEXT RULES'),nl,

    pick(_Number),

    findrule(_Number,_Name,_Preconditions,_Negative_preconditions),

    executerule(_Number,_Name,_Preconditions,_Negative_preconditions),

    !,

    run.

    run:-

    next([]),

    write('LOOP LINEAR'),nl,

    findrule(_Number,_Name,_Preconditions,_Negative_preconditions),

    executerule(_Number,_Name,_Preconditions,_Negative_preconditions),

    !,

    run.

    run:-

    nl,nl,nl, write('No rule applicable; operation halted').

    pick(_Number):-

    next([]),!,fail.

    pick(_Number):-

    retract(next([_First|_Rest])),

    eq(_Number,_First),

    assert(next(_Rest)).

    pick(_Number):- pick(_Number).

    \end{verbatim}

    For correct execution the queue next/1 must be initialised, e.g. by an empty list specification.

    Another modification and extension of the proposed mechanism can consist in assigning the rules numerical priorities and dynamic modifications of them. This can be done by specifying a proper function in the next section of any rule; then the rules can be ordered for any cycle of search with respect to current priorities.