Knowledge representation with Propositional
Logic
Propositional calculus forms the most popular logical formalism useful
in representation of models and specification of properties of numerous
systems, where the behaviour or state of elements is characterised with
binary values. An important advantage of propositional calculus consists
in simple, intuitive semantics, especially important in engineering applications.
Let us recall the bases for propositional logic. A proposition is
a finite sentence to which can be assigned its truth value: either truth
or
false.
The alphabet of the propositional calculus consists of (infinite) set of
propositional symbols, usually denoted as 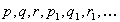 ,
etc. and a set of logical connectives. The propositional symbols are also
called atomic formulae, or atoms (for short). As logical
connectives most frequently used ones there are
,
etc. and a set of logical connectives. The propositional symbols are also
called atomic formulae, or atoms (for short). As logical
connectives most frequently used ones there are  (negation; not),
(negation; not),  (conjunction; and),
(conjunction; and),  (disjunction; or),
(disjunction; or), 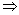 (implication;
if...then...),
and
(implication;
if...then...),
and  (equivalence; if
and only if). Sometimes special connectives are also used, but all
special functions can be expressed as appropriate combinations of the above.
More precisely, any minimal but so-called functionally complete set of
logical connectives is sufficient for expressing any logical function in
propositional calculus. Examples of such minimal but functionally complete
sets are
(equivalence; if
and only if). Sometimes special connectives are also used, but all
special functions can be expressed as appropriate combinations of the above.
More precisely, any minimal but so-called functionally complete set of
logical connectives is sufficient for expressing any logical function in
propositional calculus. Examples of such minimal but functionally complete
sets are 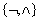 or
or 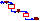 ,
while conjunction and disjunction only is not functionally complete set.
The reason for using more than a minimal functionally complete set of connectives
is the tradition and simplification of forming more complex functions.
Moreover, use of more functions and parentheses improves readability.
,
while conjunction and disjunction only is not functionally complete set.
The reason for using more than a minimal functionally complete set of connectives
is the tradition and simplification of forming more complex functions.
Moreover, use of more functions and parentheses improves readability.
The formulae of propositional logic are defined inductively as follows:
any propositional symbol p is a formula,
if 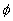 and
and 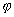 are formulae, then
are formulae, then 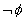 ,
, 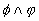 ,
, 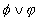 ,
, 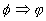 and
and 
are also formulae.
Nothing else is a formula. Sometimes, parentheses are used in order
to establish the priorities of logical operators; if no parentheses appear
in a formula (subformula), then normally the priorities are decreasing
from negation to equivalence in the shown above order.
The semantics of predicate calculus is also quite simple. Evaluation
of the so-called truth-value of a formula can be performed as soon
as the propositional formulae are individually assigned to be either true
or
false.
For simplicity, the two truth values are also denoted with
1 and
0, T and F, etc.
The practical way of evaluating the truth value of more complex formulae
is defined with the following table:
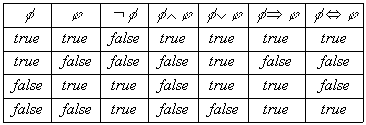
If a formula is evaluated to true under certain assignment
of truth values to propositional symbols occurring in this formula, it
is said that the formula is satisfied under this assignment (interpretation).
A formula true under any such assignment is called valid one or
a tautology. A formula which is always evaluated to false, disregarding
the assignment of its propositions is called unsatisfiable. If there
exists at least one assignment such that the formula is satisfied, it is
called a satisfiable one. In order to evaluate the truth value of
any formula one should apply the rules given in the table inductively up,
until evaluation of the total formula is generated.
To denote the fact that some formula 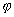 is always true (a tautology) the following notation is used: Æ
is always true (a tautology) the following notation is used: Æ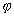 .
For example,
.
For example, 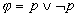 is such a
formula, i.e. Æ
is such a
formula, i.e. Æ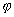 .
Another( example of a tautology is
.
Another( example of a tautology is 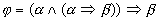 .
Further, let us consider two formulae
.
Further, let us consider two formulae 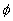 and
and 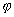 (perhaps having some
common propositional symbols occurring in them). If any assignment satisfying
(perhaps having some
common propositional symbols occurring in them). If any assignment satisfying 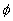 also satisfies
also satisfies 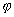 then such
fact is denoted as
then such
fact is denoted as 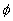 Æ
Æ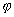 and it is said that
and it is said that 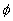 logically
entails
logically
entails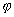 or
or 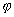 is said to be a logical consequence of
is said to be a logical consequence of 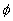 .
For example,
.
For example, 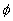 Æ
Æ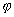 for
for 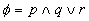 and
and 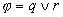 .
.
Propositional calculus can be used for model building, especially for
systems the elements of which exhibit two stable states to be distinguished
(bi-stable elements). Such elements include any mechanical, electrical,
hydraulic or pneumatic, etc. element of type rely, digital circuits, and
similar systems. Also, systems of more complex nature, but such that their
behaviour is abstracted to observed symptoms encoded with propositional
symbols.
The alphabet of first-order logic consists of symbols denoting
objects (constants), functions and relations, logical connectives, quantifiers,
and auxiliary elements, like parentheses and comma. Constants denote specific
objects, values, or phenomena. Variables are used to denote the same elements
in case the precise name of an element is currently not known, unimportant,
or a class of elements is to be represented. Simultaneously, variables
play the role of coreferrence constraints, i.e. two or more occurrences
of the same variable in an expression denote the same object; if any replacement
of the variables take place, all the occurrences of a single variable must
be replaced with the same symbol. Function symbols denote, in general,
mappings; however, they can be applied to form record-like structures for
representing more complex objects. In this case, one can assume that a
function maps its arguments into the resulting structured object. Predicate
symbols are used to specify relations holding for certain objects. The
represented relations can have no arguments (and thus they are the same
as propositional symbols describe earlier) or can take one or more arguments.
For intuition, the meaning is that the relation holds for the specific
arguments.
In the presented notation variables are denoted with single characters
or strings, always beginning with an upper case letter or underscore, constants
are denoted with any other strings of characters and special symbols or
single letters (most typically a sequence of lower-case letters and possibly
underscore characters; this convention is used in order to improve readability).
Functions and predicates are to be denoted with any arbitrary characters
or strings; they are easily recognisable by their position in any expression.
Further, proper names will be used frequently so as to provide some intuitions
and refer to some specific examples at hand. If necessary, indices will
be occasionally used, so as to provide relatively precise definitions and
theorems.
Any function and predicate symbol is assumed to take a pre-specified
number of arguments. If for some function symbol f (predicate symbol
p)
the number of arguments is n, the appropriate symbol is called an
n-place
or n-ary function (predicate) symbol. The number of arguments of
any function or predicate (its arity) can be zero or any positive
integer; however, by convention, all the 0-place functions are regarded
as constants.
The logical connectives used are, in principle, limited to the same
as in the case of propositional calculus (i.e. 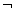 (negation; not),
(negation; not), 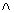 (conjunction; and),
(conjunction; and), 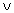 (disjunction; or),
(disjunction; or), 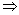 (implication;
if...then...),
and
(implication;
if...then...),
and  (equivalence; if
and only if)). Further, logical quantifiers
(equivalence; if
and only if)). Further, logical quantifiers 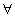 (universal quantifier) and
(universal quantifier) and 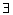 (existential quantifier) may also be used. All the logical connectives
and quantifiers can be used in order to construct more complex logical
expressions, i.e. formulae.
(existential quantifier) may also be used. All the logical connectives
and quantifiers can be used in order to construct more complex logical
expressions, i.e. formulae.
For representing any objects in predicate logic the notion of term
is necessary. A term is any constant, any variable, and any expression
of the form 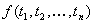 , where f
is
an n-ary functional symbol and
, where f
is
an n-ary functional symbol and 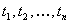 are terms; the definition then inductive. For example, the following expressions
are well-constructed terms: on, off, input_1, output_3,
switch(input_1,output_1,output_2),
distance(state,goal),
etc. The precise meaning of a term is always to be defined in particular
context by assigning the intended interpretation. For simplicity, the mes
of functional and constant symbols are selected so that they simplify the
interpretation.
are terms; the definition then inductive. For example, the following expressions
are well-constructed terms: on, off, input_1, output_3,
switch(input_1,output_1,output_2),
distance(state,goal),
etc. The precise meaning of a term is always to be defined in particular
context by assigning the intended interpretation. For simplicity, the mes
of functional and constant symbols are selected so that they simplify the
interpretation.
Basic formulae of predicate logic are atomic formulae (atoms,
for short). An atomic formula is always of the form 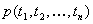 ,
where p is an n-argument relation and
,
where p is an n-argument relation and 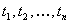 are terms. Atomic formulae in predicate logic correspond to atom of propositional
calculus. The truth assignment to atomic formulae is basically performed
by checking if the specified relation p holds for objects defined
by the terms
are terms. Atomic formulae in predicate logic correspond to atom of propositional
calculus. The truth assignment to atomic formulae is basically performed
by checking if the specified relation p holds for objects defined
by the terms 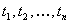 . Some example
atomic formulae can be holds(signal, on), status(switch_1,off),
or connected(input_1,switch(input_1,output_1,output_2),output_2). Positive
atomic formulae such that no variables occur in them are usually referred
to as facts.
. Some example
atomic formulae can be holds(signal, on), status(switch_1,off),
or connected(input_1,switch(input_1,output_1,output_2),output_2). Positive
atomic formulae such that no variables occur in them are usually referred
to as facts.
More complex formulae are formed from atomic ones almost exactly as
in the case of propositional calculus. The only difference consists in
the use of quantifiers. If a variable occurs inside an atomic formula,
then it is called a free variable. Such a variable has no defined
meaning and thus it would be difficult to assign some truth value to such
an atom. The use of quantifiers allows to define the "meaning" of such
a variable; if a variable occurs within the scope of a quantifier, then
it is called a bound one. In certain cases, the quantifiers are
not specified explicitly; in such a case all the variables under interest
are assumed to be implicitly existentially or universally quantified. The
most typical convention in automated theorem proving (the resolution method)
and in a logic programming language (Prolog) is that all the variables
are universally quantified (by default). In certain specific cases like
incomplete specification of state of some system, certain variables can
be implicitly existentially quantified.
In many cases variables occurring in logical expression play the role
of parameters to be replaced with specific current values. Such
replacement of variables with terms is called instantiation or - more frequently
- substitution. A substitution is any finite mapping of variables in terms.
A substitution can be conveniently represented as a set of pairs variable/term,
and thus specify explicitly which terms are substituted for which variables.
A generic form of a substitution is thus 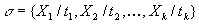 .
Such a substitution defines that variables
.
Such a substitution defines that variables 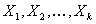 are to be simultaneously replaced with terms
are to be simultaneously replaced with terms 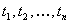 .
It is normally assumed that
.
It is normally assumed that 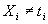 (to avoid empty substitutions) and that
(to avoid empty substitutions) and that 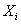 does not occur in the term
does not occur in the term 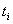 (in order to avoid problems of recursive substitutions). For example, if
(in order to avoid problems of recursive substitutions). For example, if 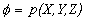 is
an atomic formula and
is
an atomic formula and 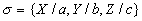 is a substitution, than the result of applying
is a substitution, than the result of applying 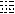 to
to 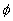 is denoted as
is denoted as 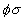 ,
and obviously
,
and obviously 
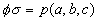 .
.
Amongst the formulae, some most useful ones are again simple formulae,
i.e. conjunctions of positive (non-negated) atomic formulae. They allow
for specification of some properties holding simultaneously. For example,
the formula  may specify
a state in which switch_1 is an, the temperature of coolant is normal and
the speed is low.
may specify
a state in which switch_1 is an, the temperature of coolant is normal and
the speed is low.
Considering two arbitrary formulae of predicate logic, say 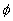 and
and 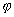 , it may be quite difficult
to verify if
, it may be quite difficult
to verify if 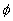 Æ
Æ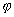 ,
i.e. if one of them logically follows from the other. Such a check however
is very frequent in practical applications. For example checking if certain
conditions do hold in current state of if preconditions of an inference
rule are satisfied. However, if the formulae are restricted to be positive
simple formulae, the check can be somewhat simplified. This is stated by
the following proposition.
,
i.e. if one of them logically follows from the other. Such a check however
is very frequent in practical applications. For example checking if certain
conditions do hold in current state of if preconditions of an inference
rule are satisfied. However, if the formulae are restricted to be positive
simple formulae, the check can be somewhat simplified. This is stated by
the following proposition.
Proposition. Consider two positive simple formulae, 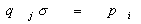 and
and 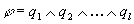 . Formula
. Formula 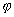 logically follows from formula
logically follows from formula 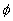 (also formula
(also formula 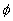 logically
entails formula
logically
entails formula 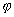 ) if and
only if there exists substitution
) if and
only if there exists substitution 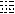 ,
such that for any fact
,
such that for any fact 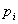 of formula
of formula 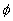 there exists
some fact
there exists
some fact 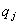 in formula
in formula 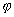 ,
such that
,
such that 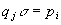 ; (in other words,
there is
; (in other words,
there is 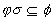 ); this is denoted
as
); this is denoted
as 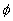 Æ
Æ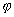 ,
and
,
and 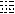 is called the match
substitution.
is called the match
substitution.
One can see that the notion of logical entailment in logical
formalism corresponds in fact to the notion of generalisation in
attributive or similar knowledge representation formalisms.

![]() ,
etc. and a set of logical connectives. The propositional symbols are also
called atomic formulae, or atoms (for short). As logical
connectives most frequently used ones there are
,
etc. and a set of logical connectives. The propositional symbols are also
called atomic formulae, or atoms (for short). As logical
connectives most frequently used ones there are ![]() (negation; not),
(negation; not), ![]() (conjunction; and),
(conjunction; and), ![]() (disjunction; or),
(disjunction; or), ![]() (implication;
if...then...),
and
(implication;
if...then...),
and ![]() (equivalence; if
and only if). Sometimes special connectives are also used, but all
special functions can be expressed as appropriate combinations of the above.
More precisely, any minimal but so-called functionally complete set of
logical connectives is sufficient for expressing any logical function in
propositional calculus. Examples of such minimal but functionally complete
sets are
(equivalence; if
and only if). Sometimes special connectives are also used, but all
special functions can be expressed as appropriate combinations of the above.
More precisely, any minimal but so-called functionally complete set of
logical connectives is sufficient for expressing any logical function in
propositional calculus. Examples of such minimal but functionally complete
sets are ![]() or
or ![]() ,
while conjunction and disjunction only is not functionally complete set.
The reason for using more than a minimal functionally complete set of connectives
is the tradition and simplification of forming more complex functions.
Moreover, use of more functions and parentheses improves readability.
,
while conjunction and disjunction only is not functionally complete set.
The reason for using more than a minimal functionally complete set of connectives
is the tradition and simplification of forming more complex functions.
Moreover, use of more functions and parentheses improves readability.

![]() is always true (a tautology) the following notation is used: Æ
is always true (a tautology) the following notation is used: Æ![]() .
For example,
.
For example, ![]() is such a
formula, i.e. Æ
is such a
formula, i.e. Æ![]() .
Another( example of a tautology is
.
Another( example of a tautology is ![]() .
Further, let us consider two formulae
.
Further, let us consider two formulae ![]() and
and ![]() (perhaps having some
common propositional symbols occurring in them). If any assignment satisfying
(perhaps having some
common propositional symbols occurring in them). If any assignment satisfying ![]() also satisfies
also satisfies ![]() then such
fact is denoted as
then such
fact is denoted as ![]() Æ
Æ![]() and it is said that
and it is said that ![]() logically
entails
logically
entails![]() or
or ![]() is said to be a logical consequence of
is said to be a logical consequence of ![]() .
For example,
.
For example, ![]() Æ
Æ![]() for
for ![]() and
and ![]() .
.