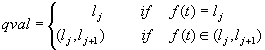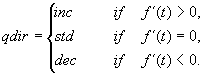4.4 Qualitative knowledge representation

Qualitative knowledge representation refers to non-numerical but still showing some order and perhaps arithmetical properties item. This section outlines the basic approaches to qualitative representations used in AI for process modelling, control, supervision and diagnosis.

 Needs for qualitative knowledge representation

One of the current most interesting research areas in Artificial Intelligence (AI) is the domain of development, analysis and application of symbolic computational methods for representation of knowledge and reasoning about the behaviour of complex dynamic systems. The most intensively explored research lines include modelling and simulation of system behaviour, system analysis and diagnosis of abnormal behaviour.
Despite the indisputable success of classical, analytical methods based on classical mathematics (e.g. differential or difference equations), there is still a need for approaches and tools for dealing with complex systems, described usually at linguistic level. Especially important is the case of imprecise and incomplete knowledge. In such case AI approaches based on observation of human behaviour and heuristics are potential solution candidates.

There are a number of particular formalisms for qualitative reasoning about dynamic systems. Some review of currently investigated proposals can be found in [Dague, 1995].

In the following subsection one of the most popular and mathematically most elegant formalism of Kuipers [Kuipers, 1986] is outlined. In certain sense the formalism is an extension of the other formalisms using just algebra of signs (i.e. the qualitative space is limited to three elements, {-,0,+}. The main extension here consists in admitting the division of the qualitative space into an arbitrary number of intervals by defining the so-called landmark values. As an approach to simulation, it can be regarded as a specialised rule-based approach. Further, extensive use of constraints allowing for reduction of the number of behaviour prediction seems to constitute another important characteristics of the presented approach.

First however, we start with presentation of some basic problems of imprecise calculations based on interval calculus. Then we present mathematical foundations of the qualitative knowledge representation and revise its potential applications.

Interval calculus problems

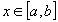In case of imprecise knowledge about some considered systems the most obvious idea is to consider its parameters to be specified with some accuracy. From mathematical point of view, instead of a precise, single-number value x one admits an interval , such that . The basic rules of interval calculus are as follows:

  • addition: ,
  • subtraction: 
  • multiplication: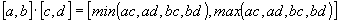 
  • division: 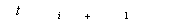, provided that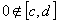 


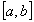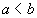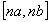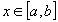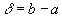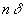    • The basic problem of interval calculus is the increase of impreciseness as the calculations go on. To notice that let us consider summation of n identical intervals , where . As the result we obtain the interval , i.e. if the accuracy of the initial parameter  was some , the accuracy of the result is equal to ; roughly speaking, this means that the result is n times less precise. In case of dynamic systems where the next state is calculated iteratively on the base of the current one, after several steps of simulation the description of state may become arbitrarily imprecise. This may make the usefulness of such kind of approach to simulation questionable.

    The basic important characteristic of the presented approach further Kuipers approach is that while using a version of the interval-based approach, the accuracy of simulation is kept within the initial quality space (in some cases new landmarks can be detected). Unfortunately, the predicted behaviour is no longer unique (despite some simple cases); furthermore, the so-called spurious behaviour predictions can be generated.

    Algebra of signs

    [JMF: to be filled - on the base of Koumana Thesis}

     Qualitative knowledge representation based on landmarks   Let us present the basic mathematical formalism underlying one of the most interesting, general and significant approaches for qualitative modelling and simulation. The approach itself was proposed by Kuipers in [Kuipers, 1986]. An important advantage of this formalism is that it is closed to control theory and, in cases of incomplete knowledge, can be applied for qualitative prediction of dynamic behaviour.

    As in control theory it is assumed that the behaviour of dynamic system to be considered is characterised by a number of real-valued parameters. The exact values of these parameters change over time. The set of these values (sometimes considered to be minimal) at a certain point of time constitutes the so-called state vector. The set of all the values of state vector

    over time constitutes the system trajectory or history.

    Any physical parameter of the considered system is assumed to be a function of the form:
     
     

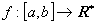    where is the extended real number line. Both the domain and range of function f are assumed to be closed intervals included in the extended set of real numbers , i.e. .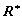

    In the following it is assumed that any considered function f is the so-called reasonable function, i.e. one which is continuous over its doma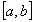in (), continuously differentiable inside its domain (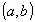), it has only countably many critical points over any bounded interval, and the first derivative is right hand continuous at a and left hand continuous at b. The first and second point constitute requirement that f should be sufficiently regular, i.e. continuous and smooth. The third one excludes functions whose behaviour changes infinitely quickly around some points. The fourth requirement is necessary for excluding pathological behaviour around the endpoints of the domain interval.

    In order to define qualitative behaviour of a reasonable function any such function is assigned a set of characteristic values, to be called landmarks. Every reasonable function 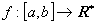 has associated with it a set of landmark values. The landmark values are assumed to include 0, f(a), f(b), as well as the value of f(t) for any critical point; they may cover any number of additional values.

    Further, specific time points associated with the landmark

    values are distinguished; 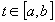 is a distinguished time point of f iff t is a boundary element for a subinterval of 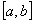, for which f is equal to some landmark value. For intuition, distinguished time points describe instants of time when something important happens to the value of, e.g. passing a landmark value or reaching an extremum.

    A reasonable function has a finite set of distinguished time points:
     
     

    and a finite set of landmark values:
     
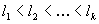      For the rest of the considerations a basic assumption is that the qualitative behaviour of a system can be described with use of landmark values and the sign of the first derivative only, i.e. the

    precise values of f are replaced with a set of points and intervals; in this way more abstract, qualitative representation is introduced. For any 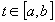,  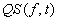is defined to be the so-called qualitative state of f at t, where  defined as follows:
     
     

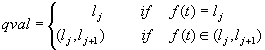    and
     
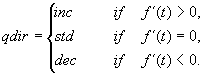      Thus the qualitative state of a single-parameter system is described with the qualitative value of this parameter, being a landmark value or an interval, and the sign of its first derivative indicating the direction of changes. Note that the qualitative state defined as above remains stable between any distinguished time points; this is so because its value qval remains between two neighbouring landmarks (or it remains stable at the value of the same landmark) and its qualitative derivative cannot change its value between neighbouring distinguished time points. 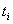Hence, for adjacent time points  and 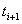 one can define the qualitative state  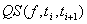on the interval  as simply 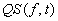 for any 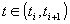. The qualitative behaviour of f on 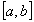 is therefore the sequence of its qualitative states:
     
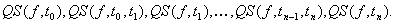      Further, one can define the qualitative state for a set of reasonable functions as follows. Let 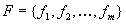 be a set of reasonable functions, where each . Let the set of distinguished time points of F be the union of the sets of distinguished time points of all the individual functions; any function 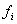 can have its own, individual set of landmark values. The qualitative state of a system F of m functions is the m-tuple of qualitative states of individual functions:
     


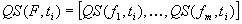
    The qualitative behaviour of F is the appropriate sequence of qualitative states:
     

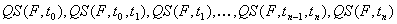    The sequence above forms a qualitative trajectory of the system. Any state of a dynamic system characterised by a set of reasonable functions representing the changes of its parameters over time has a precisely defined qualitative description QS(F,t). Since the qualitative representation changes only at discrete distinguished time points and remains constant on open intervals between them, by ''next state'' we shall understand next distinct qualitative state of the considered system.

    In monitoring and supervision of dynamic systems the basic issue of interest is the representation of state. Using the presented formalisms, the state of a dynamic system F composed of m functions (state variables) can be practically represented as follows. Let us select m attrib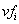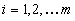utes , , such that the meaning of the i-th attribute is just the qualitative value qval of the i-th function; recall that it is either a landmark value or an interval between two adjacent landmarks. Further, let us select another m attributes 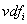, , 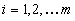each of them being interpreted as the qualitative value of first derivative qdir of the respective function; recall that its value can be just inc, std, or dec, depending on if the function is increasing, steady or decreasing, respectively. Let t denote any time instant. Using the attributive knowledge representation a simple conjunctive formula representing qualitative state of the system (parametrized with t) can be represented as follows:
     

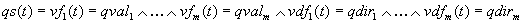    For intuition, it is convenient to imagine any qualitative state as a small hypercube in 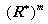 whose dimensions are defined by the values 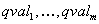 (expressed with some single or adjacent landmark values) together with a vector 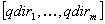 assigned to it. Any more general formula, corresponding to "enlarging" the hypercube by extending the boundaries of certain dimension (any two landmarks, not just adjacent ones) and/or admitting more than one value of some 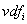 will correspond to qualitative situation and will cover several qualitative states. For intuition, it will correspond to a larger hypercube with, roughly speaking, less precisely determined the vector of qualitative derivatives values.