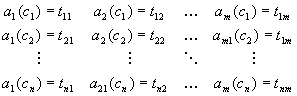4.3 Symbolic data representation
In this section knowledge representation with the use of attributes
is outlined. Such type of knowledge representation seems to be prevailing
in knowledge engineering due to its simple, intuistic interpretation and
wide applicability. Although the particular form of displaying information
(notation variants) may be different, the formalism is basically the same
over numerous knowledge representation formalisms. In general, it is applicable
to both qualitative and quantitative data. Below a simple, generic form
and its extensions are presented.
Simple knowledge representation with attributes
Let C denote a set of objects (elements) of interest; in case
of supervision these are usually the subsequent states. These can also
be physical components of the considered system or abstract concepts like
performance indices characterising system behaviour. The elements of C
will be further described by providing values of some attributes
applicable to their characterisation. Attributes are just any preselected
properties taking specific values at certain instants of time.
Let A denote a set of attributes selected to describe important
features of the system under consideration, 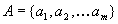 .
For any attribute
.
For any attribute 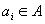 let
let 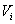 denote a (finite) set of possible values of this attribute, or in case
of real or integer numbers let it be some interval. For avoiding triviality,
it is assumed that any set
denote a (finite) set of possible values of this attribute, or in case
of real or integer numbers let it be some interval. For avoiding triviality,
it is assumed that any set 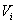 contains at least two different elements. Further, functional character
of the attributes is assumed, i.e. at some instant of time for any object
contains at least two different elements. Further, functional character
of the attributes is assumed, i.e. at some instant of time for any object 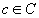 ,
if
,
if 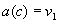 and
and 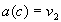 then
then 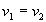 .
.
Moreover, for the sake of simplicity it is assumed that any attribute
is applicable to any object; an extension to a more general case where
any object has a specific sets of attributes applicable to it is straightforward.
The values of an attribute can be just listed in a set, or some order of
them may be established.
A basic knowledge representation item consists of specification of some
element 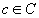 , its attribute
, its attribute 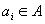 and
a value of this attribute. Such a triplet constitutes a fact; in
logical terms it constitutes an atomic formula. For intuition, the
meaning of such a formula is that the value of the specified attribute
for a given element is just the one provided; thus the basic relation here
is equality, taken in the sense of assignment of a value to a function.
Thus the basic atomic formula is always of the form:
and
a value of this attribute. Such a triplet constitutes a fact; in
logical terms it constitutes an atomic formula. For intuition, the
meaning of such a formula is that the value of the specified attribute
for a given element is just the one provided; thus the basic relation here
is equality, taken in the sense of assignment of a value to a function.
Thus the basic atomic formula is always of the form:
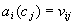 where
where 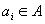 is an attribute,
is an attribute, 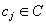 is an object to be characterised, and
is an object to be characterised, and 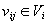 is the value of the attribute for the given object
is the value of the attribute for the given object 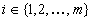 ,
, 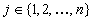 and . One can also admit partially specified facts of the form
and . One can also admit partially specified facts of the form
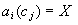 where X is a variable; in this case the value of the attribute is
not specified.
where X is a variable; in this case the value of the attribute is
not specified.
For example, colour(light) = red denotes the fact that the value
of attribute colour for light red. For attribute such
as temperature and object being coolant a fact like, for
example temperature(coolant) = upper_limit might denote some dangerous
situation when the temperature of cooling liquid reaches some predefined
upper limit. For numeric variables the representation is similar, e.g.
in order to denote the fact that current speed amounts to 60 (typically
written as v=60), one can construct the description value(speed)=60.
Note that when characterising one, specific object, the specification
of its attributes can be even simpler, i.e. it can take the form:
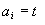 where t is the specific value of the attribute or a variable (if
the value is unknown).
where t is the specific value of the attribute or a variable (if
the value is unknown).
If the values of two or more attributes are specified, then such a specification
forms the so called conjunction of facts, a notion imported from
logic. A conjunction represents a set of facts holding simultaneously.
Such a conjunction of facts will be called also a simple fact formula
or simple formula for short. Conjunction is denoted with the symbol  .
A simple formula is always of the form
.
A simple formula is always of the form 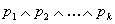 ,
where any
,
where any 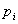 is a fact.
is a fact.
Knowledge representation with attributes is sometimes called the Object-Attribute-Value
(OAV) or the Attribute-Object-Value (AOV) formalism.
Simple formulae characterise current state of a system (a more detailed
discussion, definitions and a formal treatment of the problem of logical
state representation has been described in the former section around in
this paper). Since a simple formula constitutes in fact an abstract characterisation
(usually only selected parameters/features are taken into account), as
we mentioned it can in fact refer to a situation including a great number
of real states.
If all the attributes apply to all objects, a complete formula characterising
all the values of the attributes for all the objects displayed in form
of "linear" conjunction would be clumsy and perhaps difficult to read;
in such a case a tabular representation is much more transparent. A tabular
form of such simple formula can look as follows:
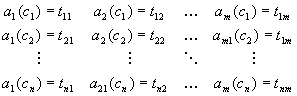 where
where 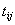 is a defined value
or a variable. If all the values of attributes are specified explicitly,
the formula represents somewhat maximal information. In case some of the
attributes have unspecified value for certain object the tabular representation
can be reduced.
is a defined value
or a variable. If all the values of attributes are specified explicitly,
the formula represents somewhat maximal information. In case some of the
attributes have unspecified value for certain object the tabular representation
can be reduced.
In practice, some of the attributes may be unimportant or inapplicable
to certain objects (e.g. the colour of certain elements may be not
important and thus not specified (for example the weight is an attribute
not applicable to an element like light). In the first case one
can use the sign "_'' while in the second one the "*
". Such a weakened description forms a more general (abstract) formula.
It is often still more convenient to use a simplified tabular form similar
to tables in relational databases. In such a form the columns are marked
with attributes, while any row provides description of certain object.
The simplified tabular form is still more readable and it allows not to
repeat the names of the attributes and the names of the objects. The form
is as follows:
Extended knowledge representation with attributes
In this subsection an extended language for knowledge representation
with use of attributes is presented. The basic extension consists of admitting
imprecise characterisation of the values of attributes for certain objects
by allowing for the use of sets. It is no longer assumed that the value
of certain attribute for a given object is given precisely. As a generalisation
a
set of possible values is specified rather than single value.
As in the former section let C denote a set of objects (elements)
of interest. The elements of C will be described by providing values
or sets of values of some attributes applicable to their characterisation.
Let A denote a set of selected attributes, 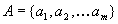 .
For any attribute
.
For any attribute 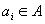 let
let 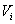 denote a (finite) set of possible values of this attribute. As before,
functional character of attribute values is assumed and for simplicity
it is assumed that any attribute is applicable to any object.
denote a (finite) set of possible values of this attribute. As before,
functional character of attribute values is assumed and for simplicity
it is assumed that any attribute is applicable to any object.
As an extension with respect to the former subsection, a basic knowledge
representation item (fact, atom) consists of any element, an attribute
selected to describe it and a set of possible values of this attribute
(if applicable). Such a specification of knowledge item is still called
a fact or atomic formula (atom, for short). For intuition,
the meaning of such a fact is that the value of the specified attribute
for a given element is equal to one of the elements of the specified
set. Hence the basic relation here is inclusion and the standard form of
any atomic formula is always as follows:
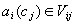 where
where 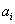 is an attribute,
is an attribute, 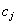 is an object to be characterised, and
is an object to be characterised, and 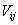 is the set of possible values of the selected attribute
is the set of possible values of the selected attribute 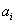 for object
for object 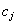 . Of course,
. Of course, 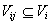 ,
i.e.
,
i.e. 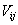 is a subset of the
predefined set of possible values of attribute
is a subset of the
predefined set of possible values of attribute  .
For simplicity the case of variables used to specify the set of admissible
values is not further considered here.
.
For simplicity the case of variables used to specify the set of admissible
values is not further considered here.
Note that from a formal point of view facts defined as above are not
a direct subclass of atoms in pure first order logic; with respect to the
intended interpretation, since sets are used as arguments, specific reasoning
mechanisms should be applied. For example, given two facts as  and
and 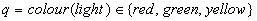 no
purely logical reasoning mechanism would be able to deduce q from
p, i.e. to show that pÆ q
(where
Æ
is the symbol denoting logical consequence). In order to do this, one should
transform the above atoms into "equivalent" logical formulae of the form
no
purely logical reasoning mechanism would be able to deduce q from
p, i.e. to show that pÆ q
(where
Æ
is the symbol denoting logical consequence). In order to do this, one should
transform the above atoms into "equivalent" logical formulae of the form 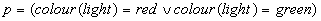 and
and 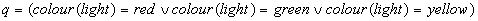 respectively.
The meaning of an element belonging to a set of possible values is that
some of the values is taken, i.e. it corresponds to logical disjunction
(
respectively.
The meaning of an element belonging to a set of possible values is that
some of the values is taken, i.e. it corresponds to logical disjunction
( ). Such a transformation, however,
would lead normally to clumsy and long expressions, and in some cases it
may be impossible (i.e. if the specified set is infinite). Thus specific
inference rules should be provided.
). Such a transformation, however,
would lead normally to clumsy and long expressions, and in some cases it
may be impossible (i.e. if the specified set is infinite). Thus specific
inference rules should be provided.
Depending on the current needs one can admit various notation possibilities,
e.g. if the set of values for attribute a is ordered, one can use
typical algebraic symbols as  ,
, 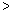 ,
, 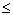 ,
, 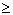 .
For example, if
.
For example, if 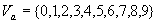 , then
the fact
, then
the fact 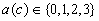 can be denoted
as
can be denoted
as 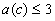 , etc.
, etc.
Note that for several facts having the same object and attribute but
different sets of values, a partial order relation can be established.
A more general fact will admit a wider set of possible values. The following
definition introduces formally the concept of generalisation.
Definition. Consider two facts 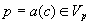 and
and 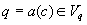 . Fact q is
said to be more general than fact p (also fact p is said
to be more specific than fact q) if and only if
. Fact q is
said to be more general than fact p (also fact p is said
to be more specific than fact q) if and only if 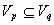 .
.
Note that if the appropriate set is not specified (i.e. an unconstrained
variable is given), then one can replace it with the domain of the attribute,
i.e. the set 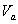 and the generated
atomic formula is equivalent to the former one. This kind of convention
can be used to simplify further consideration. Note that a more general
fact logically follows from a more specific one (i.e. pÆ
q) provided that the specific interpretation referring to the appropriate
sets of values is considered.
and the generated
atomic formula is equivalent to the former one. This kind of convention
can be used to simplify further consideration. Note that a more general
fact logically follows from a more specific one (i.e. pÆ
q) provided that the specific interpretation referring to the appropriate
sets of values is considered.
The above definition allows for simple check of generalisation amongst
facts, provided that the appropriate sets are given explicitly. In case
the sets are specified implicitly, specific, case-dependent reasoning procedures
should be applied. For example, if the sets are specified as intervals,
interval inclusion should be verified; this can be done by comparison of
their boundary values.
As before, several single facts can be used to form simple conjunctive
formulae. Similarly to the former subsection, array (tabular) representation
of simple fact formulae can be admitted. An interesting problem consists
in comparing such formulae with respect to which of two simple formulae
is more general than the other, or to check if generalisation holds. As
before, more general formula describes potentially more items, since it
imposes weaker conditions. The generalisation for simple formulae will
be defined as below.
Definition. Consider two simple formulae 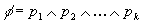 and
and 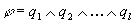 . Formula
. Formula 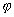 is said to be more general than formula
is said to be more general than formula 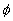 (also formula
(also formula 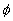 is said
to be more specific than formula
is said
to be more specific than formula 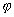 )
if and only if for any fact
)
if and only if for any fact 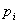 of formula
of formula 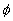 there exists
some fact
there exists
some fact 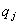 in formula
in formula 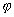 ,
such that
,
such that 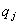 is more general
than
is more general
than 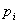 (
(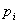 Æ
Æ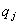 ).
).
Note that generalisation defined as above is equivalent to logical entailment,
i.e. a more general formula logically follows from a more specific one;
thus the notation 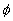 Æ
Æ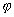 will also be used.
will also be used.
In the above definition it is assumed that both the above formulae are
specifically reduced, i.e. no two facts in a single formula refer to the
same combination of object an attribute. For example, if 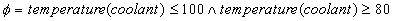 then reduced (but equivalent) form of
then reduced (but equivalent) form of 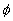 would be
would be 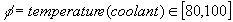 . One can see
that for simple formula
. One can see
that for simple formula 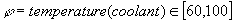 the generalisation was not holding according to for the non-reduced form
of
the generalisation was not holding according to for the non-reduced form
of 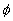 ; however for reduced
form there is
; however for reduced
form there is 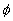 Æ
Æ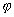 ,
since
,
since 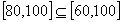 . From now on only
reduced forms of simple formulae will be considered.
. From now on only
reduced forms of simple formulae will be considered.
Checking if generalisation holds for simple formulae is a crucial test
in situation recognition, checking if precondition of certain formula are
satisfied, etc. Hence, the definitions introduced in this section constitute
an important foundations for inference in knowledge based systems.

![]() .
For any attribute
.
For any attribute ![]() let
let ![]() denote a (finite) set of possible values of this attribute, or in case
of real or integer numbers let it be some interval. For avoiding triviality,
it is assumed that any set
denote a (finite) set of possible values of this attribute, or in case
of real or integer numbers let it be some interval. For avoiding triviality,
it is assumed that any set ![]() contains at least two different elements. Further, functional character
of the attributes is assumed, i.e. at some instant of time for any object
contains at least two different elements. Further, functional character
of the attributes is assumed, i.e. at some instant of time for any object ![]() ,
if
,
if ![]() and
and ![]() then
then ![]() .
.
![]() , its attribute
, its attribute ![]() and
a value of this attribute. Such a triplet constitutes a fact; in
logical terms it constitutes an atomic formula. For intuition, the
meaning of such a formula is that the value of the specified attribute
for a given element is just the one provided; thus the basic relation here
is equality, taken in the sense of assignment of a value to a function.
Thus the basic atomic formula is always of the form:
and
a value of this attribute. Such a triplet constitutes a fact; in
logical terms it constitutes an atomic formula. For intuition, the
meaning of such a formula is that the value of the specified attribute
for a given element is just the one provided; thus the basic relation here
is equality, taken in the sense of assignment of a value to a function.
Thus the basic atomic formula is always of the form:
![]() .
A simple formula is always of the form
.
A simple formula is always of the form ![]() ,
where any
,
where any ![]() is a fact.
is a fact.