Knowledge representation - critical evaluation
of logic-based approaches
In this section we present argumentation that any kind of knowledge
representation language is nothing but another syntax, or ''syntactic sugar''
over logic, and as such could be avoided be replacement by logical knowledge
base. On the other hand we argue that there is necessity for diversity
of knowledge representation formalism, incorporating extra-logical features,
as spatial and temporal composition, structural displaying, hierarchical
presentation, etc.
First let us briefly comment on existing knowledge representation techniques
and show that practically all of them are just based on logic, sometimes
with syntactic addition termed sometimes to be ''syntactic sugar''. Classical
books on AI list usually the following knowledge representation schemes:
object-attribute-value items, i.e. O-A-V facts,
logic, mostly understood as first-order predicate calculus,
production rules, or more precisely rule-based systems,
frames, sometimes termed ''semantic.....''; objects (in object oriented
programming may be also considered as kinds of frames and vice versa),
semantic graphs in various forms, where nodes represents objects
and links relations among them,
scenarios, especially for dynamic systems
Some most popular and useful in supervision systems techniques were
recapitulated in this Chapter. Note that obviously various mixtures of
the methods are also possible.
Let us briefly review the above methods in context of logic.
The object-attribute-value facts are just another syntax of logic. Note
that a fact like a(c)=v, denoting the fact that the value of attribute
a
for object c is equal to v can be presented in logic as an
atomic formula equal(a(c),v), or holds(fact(a(c),v)), etc.
Moreover, using logic one can easily encode three-, four-,
and n--ary relations, as between(two,one,three) or four_in_order(1,2,3,4)
which is not necessarily so easy in the O-A-V formalism. Further, logic
provides a way of representing lists, and thus dealing with sets and sequences
becomes possible; a list [a,b,c,d] is a shorthand for .(a,.(b,.(c,.(d)))),
where ./2 is a binary functional symbol selected for crating lists
(as in LISP-like languages) and infix notation is applied.
With respect to rules, let us consider the basic rules of the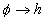 
where 
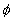is the precondition and 
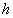is conclusion; from logical point of view such a rule can be represented
as implication 
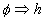, which,
when applied (e.g. with modus ponens inference principle) produces effect
equivalent to application of the corresponding production rule.
Coming to frames one should take a look at the structure of this construct.
Frequently, it consists of specification of certain object description
with facets and slots and an operational part answering the questions like
if-needed,
if-added,
if-modified,
etc. The first part is usually as a record-like structure, forming some
hierarchy, and providing certain values characterising the described object.
This can be perfectly represented with an arbitrarily complex term structure,
following the pattern:
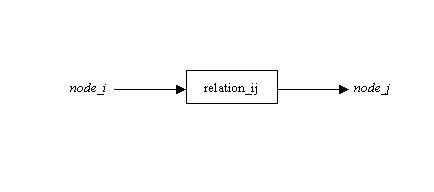
which is the basic connection of the graph. Obviously, it can
be modelled as an atomic formula relation_ij(node_i,node_j), or,
even more generally as holds(relation_ij,node_i,node_j). The whole
graph can be modelled as a set (logically: conjunction) of such statements;
further, some auxiliary descriptors can be added as additional parameters..
To complete the picture let us mention some specific features of logic,
hardly encountered in other formalisms. Logic has clearly defined syntax
and semantics. An important thing is that logic is not only knowledge representation
formalism, but it is also a tool for knowledge processing; automated deduction
provides the framework for problem solving. Further, deduction rules posses
the property of producing valid output, i.e. only correct output is generated.
And last but not least, it is not difficult to provide a deduction system
which is complete, i.e. if a formula (solution, hypothesis, etc.) follows
from the axioms, then it (or its generalised form) can be deduced from
the axioms within the system; in simple words, if the solution exists,
it can be found.
The question is: if the picture of logic so positive, should we, and
- if so - why, consider another knowledge representation formalism? In
other words why - if - logic is not sufficient for knowledge representation,
what are the shortcomings and how to improve the situation, i.e. what additional
features should the knowledge representation mechanism posses?
The answer to this question is, as usual, complex and somewhat subjective.
But in supervisory knowledge-based system, especially ones involving human
operator, man-machine co-operation and expert co-operation, the answer
to these question comprises a crucial factors for design and implementation
of useful, user friendly systems.
Below, a list of features considered to be drawbacks of classical logic
is presented:
Difficult, sometimes ambiguous syntax, hardly acceptable by human process
operators. This follows from the fact that we were taught to fink functionally,
i.e. in term: the result of this is that, but not relationally,
i.e. this relation holds for these objects. we were all mostly taught maths,
not logic.
People often think basing on physical intuition; a common phenomenon likely
to use in reasoning is causality. Logic, itself allows for specification
of causal dependencies, but does not provide any mechanism for intuitive
representation and dealing with causality; the order (positions) of arguments
in predicates is not enough to do that.
People often specify and use hierarchical dependencies for representing
knowledge. Again, logic is ''flat'', it does not support dealing with hierarchy
in a simple, natural way.
Logical formulae have, flat monotonous structure, all elements are equally
important; people like to present information in a structural form which
helps to perceive and comprehend the represented knowledge.
Logic has no display form: visual representation is important to people,
most of the information (above 80\%) comes through eyes in the form of
images. Spatial presentation makes easier and more readable knowledge representation.
Furthermore, spatial relations may directly model certain important relationship,
e.g. in graphs, the distance between nodes may model the real distance
between towns. Spatially displayed information helps to quickly perceive
and analyse certain global features, e.g. existence of connections, area,
shape, etc. Tabular displays help arrange and order knowledge.
Logic is inflexible, and thus hard to specify specific aspects of knowledge,
such as uncertainty, vagueness, fuzziness, strength, etc.
Logic is far from everyday tools, too general, while for specific tasks
we need more specific tools (graphs, pictures, colours, etc.),
Classical logic does not cover directly default and nonmonotonic inference,
and thus modelling these issues is practically difficult.
It is difficult to control the deduction strategies; combinatorial explosion
easily occurs, and the way of knowledge presentation (syntax) does not
help here. Sometimes, answers to simple questions are very hard to find.
Logic does not support calculation in a simple and direct way; this however
is often the basic necessity.
Logic does not support directly qualitative inference, very important while
dealing with imprecise information and reasoning at higher abstract levels.
Finally, logic is strict, and if inconsistency occurs, it turns out to
be useless (an error); in the meantime, certain types of inconsistencies
are part of everyday' practice and human easily handle them.
The above points summarise only some most crucial lacks of classical logic.
Many of the points are touched or solved by modern types of extended or
modified logic, such as fuzzy logic, multivalued logics, nonmonotonic logics,
etc.
Some graphical tools for supporting knowledge representation include:
flow charts, flow diagram, flow graphs, etc., covering symbolic representation
of signal flow and transformation over the system,
functional schemes, including realistic graphical representation of system
components (technological flow diagrams),
state transition graphs,
decision trees, binary trees,
decision tables,
relational (attribute-value) tables,
graphical representation of process variables, etc.
It should be noted that for more complex systems only appropriate combination
of knowledge representation techniques best fitting the characteristics
of the system to be supervised and the current specific requirements can
provide satisfactory results. Further, graphical user interface with components
of intelligent knowledge processing constitutes nowadays a compulsory component
of any knowledge based system.
