4.12 Representation of knowledge over time: episodes
Events: logical and temporal characteristics
An episode is a useful linguistic term for denoting the fact
that ''something of interest has happen and it lasted for certain period
of time''. In process monitoring, supervision and diagnosis the use of
predefined episodes for description of particular situations of interest
constitutes a convenient and natural way of representation and dealing
with the knowledge about the process. Although episodes refer mostly to
the observed output (or state) of the system, and are formed basing on
the expert superficial knowledge (vs. model-based one), they can be considered
as elements of abstract level modelling for system behaviour. For example,
the trajectory of a system can be described from a qualitative point of
view as a sequence of specific episode. Below a logical and temporal characterisation
of events is presented.
In many AI application reasoning about time is essential and several
techniques for the explicit representation and processing of time have
been proposed in the literature. Among them, the reified temporal logic
which seems to be most promising for prospective practical applications.
Two concepts w.r.t time used are time points or time intervals. They are
usually based on two primitive entities: instants as in MacDermott,
or intervals as in Allen's one. The basic construct 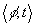 of these logics associates a formula
of these logics associates a formula 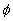 with a temporal entity t, this last is being either an instant
or an interval depending on the kind of the logic.
with a temporal entity t, this last is being either an instant
or an interval depending on the kind of the logic.
An episode consists of a propositional symbol or formula declaring some
logical property and its temporal qualification in the form of an interval
of time during which the property holds. A set (conjunction) of episodes
forms an expression (formula) containing both logical (or qualitative,
symbolic) knowledge specification and time qualification for knowledge
items. Knowledge representation with episodes is relatively simple and
intuitive. However, in certain cases such representation of knowledge can
lead to redundant and/or inconsistent) expressions of unnecessarily big
length (the knowledge is not compact).
Let us present elementary logical notions for temporal knowledge representation
and reasoning. Some most popular, simple and intuitive method for temporal
knowledge representation consists in use of episodes. An episode
provides a way of explicit representation of time duration for a proposition
of interest. It is based on positive time representation, i.e. the
intervals for which propositions hold are given explicitly; beyond these
intervals one does not know if the proposition holds or does not hold.
More formally, an episode is a pair 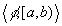 where
where 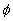 is a logical formula
or propositional symbol (or any qualitative, symbolic or numerical expression)
denoting some properties of interest (a characteristics) and where
a
and b are two real numbers, such that
is a logical formula
or propositional symbol (or any qualitative, symbolic or numerical expression)
denoting some properties of interest (a characteristics) and where
a
and b are two real numbers, such that 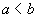 ;
; 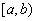 is referred to as time interval or time qualification for
is referred to as time interval or time qualification for 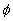 .
.
An episode constitutes a basic item for knowledge representation incorporating
time qualification. For intuition 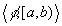 means that the property defined by
means that the property defined by 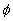 is known to hold uniformly inside the time interval
is known to hold uniformly inside the time interval 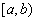 .
In general, one does not know whether
.
In general, one does not know whether 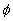 was true or not before a (a excluded) and after b
(b included). In certain particular representations one can admit
closed or open intervals, but for simplicity of the discussion the convention
of left-closed right-open intervals will be adopted; it is not generally
of interest what happens exactly before a and at and after b;
since the episode has to last for some time, the interval must be a non-zero-length
one, and the accepted convention will do. However, if necessary either
the change of intervals or the additional description at the boundary time
points can be introduced.
was true or not before a (a excluded) and after b
(b included). In certain particular representations one can admit
closed or open intervals, but for simplicity of the discussion the convention
of left-closed right-open intervals will be adopted; it is not generally
of interest what happens exactly before a and at and after b;
since the episode has to last for some time, the interval must be a non-zero-length
one, and the accepted convention will do. However, if necessary either
the change of intervals or the additional description at the boundary time
points can be introduced.
Given several episodes with the same formula 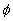 and overlapping (interacting) time intervals one may prefer to consider
only a maximal episode equivalent to the conjunction of them. Let
us recall the following idea of maximal episodes.
and overlapping (interacting) time intervals one may prefer to consider
only a maximal episode equivalent to the conjunction of them. Let
us recall the following idea of maximal episodes.
An episode 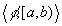 is maximal
if and only if
is maximal
if and only if 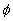 does not
hold or is unknown just before a (excluding a) and just after
b
(including b).
does not
hold or is unknown just before a (excluding a) and just after
b
(including b).
The definition stated as above is intuitive. In case of a knowledge-base
consisting of several episodes with the same propositional symbol or formula
and interacting time intervals it seems reasonable to replace them with
an equivalent maximal episode. Such an operation, to be called maximisation
or reduction yields concise representation of knowledge and can
be easily performed.
The maximisation operation is always considered within a given context,
i.e. a number (conjunction) of episodes are given. Maximisation can be
performed only for episodes having the same propositional symbol or formula
and interacting time intervals. Two intervals 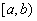 and
and 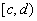 interact if and only
if the intersection of them is not empty, or they "stick" to each other,
i.e.
interact if and only
if the intersection of them is not empty, or they "stick" to each other,
i.e. 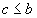 and
and 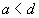 .
The maximisation operation for two episodes with interacting time intervals
is defined as follows.
.
The maximisation operation for two episodes with interacting time intervals
is defined as follows.
Let 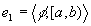 and let
and let 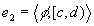 be two episodes with interacting time intervals. The maximisation operation
yields a maximal episode defined as
be two episodes with interacting time intervals. The maximisation operation
yields a maximal episode defined as 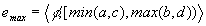 .
Obviously the maximal episode is unique and it is logically equivalent
to the conjunction of the maximised (parent) episodes. Further, maximisation
can be sequentially applied to a number of pairs of episodes in a conjunctive
formula. As the operation reduces the number of episodes in the formula,
it can be repeated only finitely many times leading to an irreducible formula.
The above operation leads in fact to reduction of the initial formula
spread over certain interacting time intervals into the simplest possible
form.
.
Obviously the maximal episode is unique and it is logically equivalent
to the conjunction of the maximised (parent) episodes. Further, maximisation
can be sequentially applied to a number of pairs of episodes in a conjunctive
formula. As the operation reduces the number of episodes in the formula,
it can be repeated only finitely many times leading to an irreducible formula.
The above operation leads in fact to reduction of the initial formula
spread over certain interacting time intervals into the simplest possible
form.
Thus one can define maximally reduced conjunctive formula as
follows.
Let 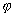 be a simple formula
(conjunction of episodes). Formula
be a simple formula
(conjunction of episodes). Formula 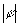 is maximally reduced form of
is maximally reduced form of 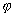 if and only if any two episodes with interacting time intervals and the
same propositional symbol have been replaced by their maximising episode.
if and only if any two episodes with interacting time intervals and the
same propositional symbol have been replaced by their maximising episode.
Obviously, in a maximally reduced (for short -- maximised or reduced)
formula no further maximisation is possible. Moreover, maximisation defined
as above is a finite operation providing unique result; the reduced form
of 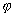 is logically equivalent
to the initial formula.
is logically equivalent
to the initial formula.
The maximisation operation is important for logical inference. Let
us consider two simple formulae 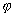 and
and 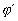 ; the problem is to
check if
; the problem is to
check if 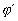 logically follows
from
logically follows
from 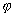 (
(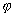 Æ
Æ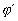 ).
).
In classical propositional calculus the above problem has a straightforward
solution (see the section on propositional calculus, the note on for positive
formulae). The test can be performed by checking if 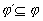 (here simple formulae are referred to as sets of propositional symbols).
In episode calculus, however, the problem is not straightforward. First,
one is to take into account the temporal qualification. It is assumed that
an episode
(here simple formulae are referred to as sets of propositional symbols).
In episode calculus, however, the problem is not straightforward. First,
one is to take into account the temporal qualification. It is assumed that
an episode 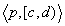 follows from
an episode
follows from
an episode 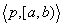 if and only
if
if and only
if 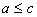 and
and 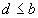 (
(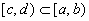 ). Further, when two episodes
). Further, when two episodes 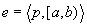
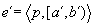 are such that
are such that 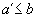 and
and 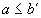 ,
they are not independent from one another. The two episodes considered
together provide, roughly speaking, more useful information then the information
provided by them considered separately. To be more precise, an episode
may follow from a set (conjunction) of episodes with interacting time
intervals, even if it does not follow from any of these episodes alone.
For instance,
,
they are not independent from one another. The two episodes considered
together provide, roughly speaking, more useful information then the information
provided by them considered separately. To be more precise, an episode
may follow from a set (conjunction) of episodes with interacting time
intervals, even if it does not follow from any of these episodes alone.
For instance, 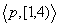 Æ
Æ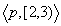 since if p holds for time interval
since if p holds for time interval 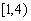 then it necessarily holds for time interval
then it necessarily holds for time interval 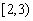 as well. Further,
as well. Further, 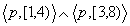 Æ
Æ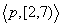 ,
but neither
,
but neither 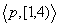 nor
nor 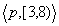 alone logically entails
alone logically entails 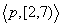 .
However, if the conjunction
.
However, if the conjunction 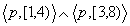 is replaced by its maximally reduced form, i.e.
is replaced by its maximally reduced form, i.e. 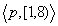 ,
, 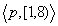 Æ
Æ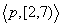 holds directly. This example shows the importance of the reduction operation
for efficient logical reasoning. In fact, the above considerations leads
to stating the following proposition:
holds directly. This example shows the importance of the reduction operation
for efficient logical reasoning. In fact, the above considerations leads
to stating the following proposition:
Proposition. Let 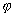 and
and 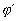 be two simple formulae
and let
be two simple formulae
and let 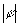 be the maximally
reduced form of
be the maximally
reduced form of 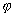 . Formula
. Formula 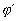 logically follows from
logically follows from 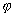 if and only if for any episode
if and only if for any episode 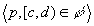 there exists an episode
there exists an episode 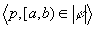 ,
such that
,
such that 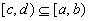 .
.
The above proposition provides a simple, algorithmic way for
checking logical entailment among simple formulae constructed with use
of positive knowledge and based on episodes. As a first step one should
maximally reduce the formula constituting the assumed knowledge. In the
second step one is to check if any episode of the tested formula is `covered'
by some episode in the reduced formula, as requested by the proposition;
both steps can be easily made algorithmic.
The idea of maximisation (reduction) of episodes implies a practical
consequence for choosing the temporal qualification when defining episodes
of interest. Obviously, the time limits defining the interval should be
selected as characteristic time points, i.e. instants of time when
the property defined by the formula 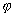 becomes true and becomes false. In other words, the episodes should be
defined so that the interval of time is maximal. This can be achieved by
selection of the time limits with respect to the definition of
becomes true and becomes false. In other words, the episodes should be
defined so that the interval of time is maximal. This can be achieved by
selection of the time limits with respect to the definition of 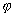 by making their definition dependent on the truth value of them formula;
thus the time extent for an episode is defined in a dependent way.
by making their definition dependent on the truth value of them formula;
thus the time extent for an episode is defined in a dependent way.
In order to define an episode typically a set of characteristic properties,
or characteristic functions should be selected. Then, a join formula
(usually a conjunction of subset of the properties) is to be established.
Finally, an episode occurs if the formula holds, and the time
interval of the episode is defined to be the time of the formula being
true. Of course, for particular needs, the time can be also defined arbitrarily,
usually as a minimal time during which 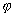 should hold in order to say that the episode has occurred.. Further details
can be found in [Bouzid and
Ligeza, 1995].
should hold in order to say that the episode has occurred.. Further details
can be found in [Bouzid and
Ligeza, 1995].
Propositional logic episodes: binary signals
A concept of episode depending on two-valued signal is briefly described
below. Consider a binary signal 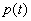 ,
taking just two values: true (1) and false (0). An episode
may consists in the signal taking the value 1 at certain time point
for in an interval of some required minimal length
,
taking just two values: true (1) and false (0). An episode
may consists in the signal taking the value 1 at certain time point
for in an interval of some required minimal length 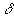 .
Let
.
Let 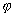 denote a propositional
formula stating that
denote a propositional
formula stating that 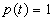 .
An episode defining that the signal is equal 1 for some period of
time may be defined as
.
An episode defining that the signal is equal 1 for some period of
time may be defined as 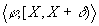 ,
where X is a variable - the time of beginning of the episode is
not defined precisely.
,
where X is a variable - the time of beginning of the episode is
not defined precisely.
This can be useful for e.g. defining more general requirements, for
example in specifying preconditions of certain actions. A description of
an episode just taking place can be 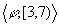 ,
i.e. the signal was equal 1 from time 3 to time 7.
Further, more complex episodes referring to combination of values of certain
signals can be defined.
,
i.e. the signal was equal 1 from time 3 to time 7.
Further, more complex episodes referring to combination of values of certain
signals can be defined.
Functional episodes
This kind of episodes refer to characteristic elements of continuous
signals, usually the output of the supervised system. Below a brief outline
of the ''classical approach of [Cheung
and Stephanopoulos, 1990a] is presented.
The proposed approach consists in analysis of time signals by abstraction
of the qualitative information in form of episodes. This allows for qualitative
analysis of process trends at the abstract level of supervision. The time
is accepted as linear, with some distinguished instants (points), and interval
of time if specified are assumed to be open, distinguished time points
are considered separately as in [Kuipers,
1986]. The qualitative state of some signal x(t) is defined
by the value of its characteristic functions, such as sign of the
function, its first derivative, and its second derivative; all the functions
are considered to be qualitative ones and taking the values + for
positive, 0 for zero and - for negative values
of x(t). Thus, a qualitative state QS(x,t) is a triple
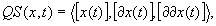 where
where 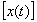 , means the qualitative
value of the function. The notion of a qualitative state can be extended
over an interval and denotes as
, means the qualitative
value of the function. The notion of a qualitative state can be extended
over an interval and denotes as 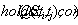 ,
provided that at any point of the interval
,
provided that at any point of the interval 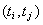 the qualitative state remains the same. An episode is then defined as a
pair
the qualitative state remains the same. An episode is then defined as a
pair 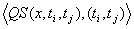 assuming that the
time interval
assuming that the
time interval 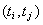 is a maximal
time interval during which the qualitative state
is a maximal
time interval during which the qualitative state 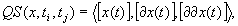 does not change (for formal reasons, this can be expressed as a logical
formula
does not change (for formal reasons, this can be expressed as a logical
formula 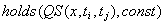 or
or 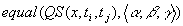 ,
just to show that this is a specific case of the general logical definition
introduced in the former section). Furthermore, the qualitative trend (or
qualitative history, qualitative trajectory) can be represented by a sequence
of non-overlapping qualitative states
,
just to show that this is a specific case of the general logical definition
introduced in the former section). Furthermore, the qualitative trend (or
qualitative history, qualitative trajectory) can be represented by a sequence
of non-overlapping qualitative states
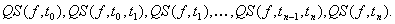
Now, basing on the notions introduce above ,a triangular episode is
defined in \cite{Cheung:90a}. The definition is refers mostly to the qualitative
value of first and second derivative, as some factors important from engineering
point of view. The precise definition states that a triangular episode
is a four-tuple 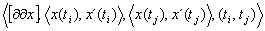 practically,
this means that a triangular episode is a triangular region contoured by
the intersecting lines of the initial slope, the final slope and the average
slope through the boundary points.
practically,
this means that a triangular episode is a triangular region contoured by
the intersecting lines of the initial slope, the final slope and the average
slope through the boundary points.
Representations of qualitative trends by triangular episodes captures
many practical requirements for qualitative trend analysis. Moreover, such
a representation is concise and essential, i.e. minimal-complete;
this means that when maximal episodes are applied, then there is no direct
repetition of the same time of episode and any trend can be described by
use of those episodes. From simple analysis it follows that there are seven
basic patterns of episodes with respect to the qualitative values of first
and second derivative, i.e. seven basic shapes (here the boundary values
are not considered so as to capture the shape only, and not the level of
signal). Another set of basic episode patterns was proposed in [Rengasamy,
1995].

![]() of these logics associates a formula
of these logics associates a formula ![]() with a temporal entity t, this last is being either an instant
or an interval depending on the kind of the logic.
with a temporal entity t, this last is being either an instant
or an interval depending on the kind of the logic.
![]() where
where ![]() is a logical formula
or propositional symbol (or any qualitative, symbolic or numerical expression)
denoting some properties of interest (a characteristics) and where
a
and b are two real numbers, such that
is a logical formula
or propositional symbol (or any qualitative, symbolic or numerical expression)
denoting some properties of interest (a characteristics) and where
a
and b are two real numbers, such that ![]() ;
; ![]() is referred to as time interval or time qualification for
is referred to as time interval or time qualification for ![]() .
.
![]() means that the property defined by
means that the property defined by ![]() is known to hold uniformly inside the time interval
is known to hold uniformly inside the time interval ![]() .
In general, one does not know whether
.
In general, one does not know whether ![]() was true or not before a (a excluded) and after b
(b included). In certain particular representations one can admit
closed or open intervals, but for simplicity of the discussion the convention
of left-closed right-open intervals will be adopted; it is not generally
of interest what happens exactly before a and at and after b;
since the episode has to last for some time, the interval must be a non-zero-length
one, and the accepted convention will do. However, if necessary either
the change of intervals or the additional description at the boundary time
points can be introduced.
was true or not before a (a excluded) and after b
(b included). In certain particular representations one can admit
closed or open intervals, but for simplicity of the discussion the convention
of left-closed right-open intervals will be adopted; it is not generally
of interest what happens exactly before a and at and after b;
since the episode has to last for some time, the interval must be a non-zero-length
one, and the accepted convention will do. However, if necessary either
the change of intervals or the additional description at the boundary time
points can be introduced.
![]() and overlapping (interacting) time intervals one may prefer to consider
only a maximal episode equivalent to the conjunction of them. Let
us recall the following idea of maximal episodes.
and overlapping (interacting) time intervals one may prefer to consider
only a maximal episode equivalent to the conjunction of them. Let
us recall the following idea of maximal episodes.
![]() is maximal
if and only if
is maximal
if and only if ![]() does not
hold or is unknown just before a (excluding a) and just after
b
(including b).
does not
hold or is unknown just before a (excluding a) and just after
b
(including b).