Results

The genetic algorithm was run on the two task complexity classes represented by the target clusters $C_{1}$ and $C_{2}$ in our simulator. The population size was of 20 individuals, and we ran the genetic algorithm for 100 generations. The initial position was the same for both tasks, with the crossover and the mutation rates being 0.8 and 0.1 respectively. In the algorithm, four of the parameters -- $\alpha$, $\beta$, $\gamma_{A}$ and $\gamma_{B}$ lie on the positive real axis and hence we have to choose an upper limit on the real line. This upper limit is important since a low upper limit value implies that we implicitly restrict our real valued parameters to that limit, while a high upper limit value may increase the number of generations for which the genetic algorithm may have to be run since the initial random generation will be very disperse. $\alpha$ and $\beta$ are exponents of numbers less than 1 and hence their large values will not be useful. Keeping these factors in consideration, the upper limit value has been fixed to 5 in our simulations.

Table 5.2: Optimal parameter values for each of the clusters for one execution of the GA over 100 generations

	$\alpha$	$\beta$	$\kappa_{1}$	$\kappa_{2}$	$\kappa$	$\gamma_{A}$	$\gamma_{B}$	$\gamma_{R}$	$\overline I_{a}$	$\overline R$
C1	1.731	2.03	0.314	0.493	0.355	0.240	0.521	0.054	0.386	0.215
C2	1.231	2.12	1.0	0.564	0.178	1.377	4.39	0.707	0.871	0.906

Figure 5.10: Fitness of the fittest individual along generations (cluster $C_1$)
Figure 5.11: Average fitness of the population along generations (cluster $C_1$)
Figure 5.12: Mahalanobis diversity (cluster $C_1$)

Figure 5.13: Fitness of the fittest individual along generations (cluster $C_2$)
Figure 5.14: Average fitness of the population along generations (cluster $C_2$)
Figure 5.15: Mahalanobis diversity (cluster $C_2$)

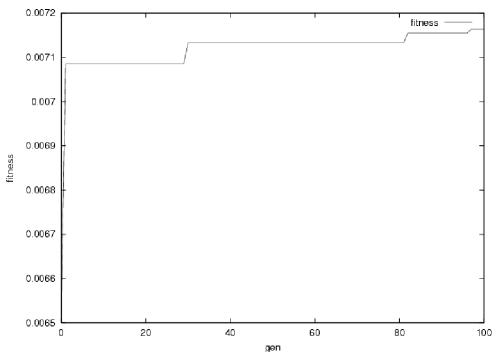
The genetic algorithm converges to an optimal solution for each cluster as can be seen in Figures 5.10-5.15. By optimal solution we refer to the best solution the algorithm has found, which may not necessarily be the optimal solution to the navigation task. The optimal values for some of the parameters differ significantly for the two clusters as shown in Table 5.2. The parameters associated to the bidding function of the Risk Manager agent differ the most between the two clusters. This is so because the Risk Manager is very sensitive to the complexity of the task. The more obstacles, the higher the risk of losing sight of landmarks.

In order to check the results obtained for each of the clusters, we have tested the two parameter sets found by the genetic algorithm on the two different navigation tasks (going to cluster $C_1$ and going to cluster $C_2$). We have also tested our original parameter set, which we set by hand, on the same two navigation tasks. The results obtained by each set on each of the tasks are shown in Table 5.3. For each task, the mean average success value ($\overline{s}$), average cost ($\overline{c}$) and the fitness value ($f$) is computed. As expected, the parameter set found for cluster $C_1$ performs perfectly when going to cluster $C_1$ and it only reaches the targets of cluster $C_2$ 50% of the time. On the other hand, the parameter set found for cluster $C_2$ reaches the targets of cluster $C_2$ all the times, while it only reaches the targets of cluster $C_1$ 50% of the time. Finally, the hand-tuned parameter set reaches 50% of the time for targets in cluster $C_1$, and never reaches the targets of cluster $C_2$. Therefore, the evolutionary approach has improved the global navigation behavior.

In Figures 5.16 and 5.17 we can see some paths followed by the robot using each of the parameter set on each of the tasks. Successful paths are only shown for those parameter set with a success value of 1. Otherwise, an example of a failing path (marked with a cross at its end) is shown.